练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，点E、F分别在AB、BC上，△DEF为等腰直角三角形，∠DEF=90°，AD+CD=10，AE=2，求AD的长．

    【答案】AD=4．

    【解析】

    试题分析：先设AD=x．由△DEF为等腰直角三角形，可以得到一对边相等，一对角相等，再加上一对直角相等，那么△ADE和△BEF全等，就有AD=BE．那么利用边相等可得x+x+2=10，解之即得AD．

    解：先设AD=x．

    ∵△DEF为等腰三角形．

    ∴DE=EF，∠FEB+∠DEA=90°．

    又∵∠AED+∠ADE=90°．

    ∴∠FEB=∠EDA．

    又∵四边形ABCD是矩形，

    ∴∠B=∠A=90°

    ∴△ADE≌△BEF（AAS）．

    ∴AD=BE．

    ∴AD+CD=AD+AB=x+x+2=10．

    解得x=4．

    即AD=4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

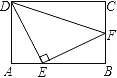
    【题目】如图1，线段AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．

    （1）求证：∠EAB=∠CED；

    （2）如图2，AF、DF分别平分∠BAE和∠CDE，EH平分∠DEC交CD于点H，EH的反向延长线交AF于点G．

    ①求证EG⊥AF；

    ②求∠F的度数．（提示：三角形内角和等于180度）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由点B向C点运动，同时，点Q在线段CA上由点C向A点运动．

    （1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由．

    （2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC．
    ①求证：DC为⊙O切线；
    ②若ADOC=8，求⊙O半径r．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某研究机构经过抽样调查，发现当地1500个老年人的养老模式主要有A，B，C，D，E五种，统计结果如图，那么下列说法不正确的是（　　）

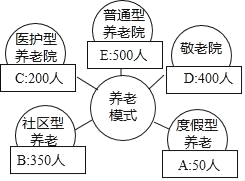
    A. 选择A型养老的频率是

    B. 可以估计当地30000个老年人中有8000人选择C型养老

    C. 样本容量是1500

    D. 总体是当地1500个老年人的养老模式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一块长方体木块的各棱长如图所示，一只蜘蛛在木块的一个顶点A处，一只苍蝇在这个长方体上和蜘蛛相对的顶点B处，蜘蛛急于捉住苍蝇，沿着长方体的表面向上爬．

    (1)如果D是棱的中点，蜘蛛沿“AD→DB”路线爬行，它从A点爬到B点所走的路程为多少？

    (2)你认为“AD→DB”是最短路线吗？如果你认为不是，请计算出最短的路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一辆慢车与一辆快车沿相同路线从地到地所行的路程与时间之间的函数图象，已知慢车比快车早出发小时，则、两地的距离为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从﹣1，0，1，3，4，这五个数中任选一个数记为a，则使双曲线y= 在第一、三象限且不等式组 无解的概率是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．

    (1)求证：△ACE≌△BCD；

    (2)若AD＝5，BD＝12，求DE的长．

    查看答案和解析>>

    同步练习册答案