
【题目】解下列一元一次方程:
(1)0.5x﹣0.7=6.5﹣1.3x (2)1﹣2(2x+3)=﹣3(2x+1)
(3)5(x+8)=6(2x﹣7)+5; (4)5﹣![]() =x
=x
(5)![]() ﹣
﹣![]() =1 (6)
=1 (6)![]() ﹣
﹣![]() =
=![]() ﹣1.
﹣1.
【答案】(1) x=4;(2) x=1;(3) x=11;(4) x=4;(5)x=0;(6)x=0.
【解析】
解一元一次方程一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.在具体的问题中,应结合方程特点灵活运用相关步骤进行求解。具体:(1)移项、合并同类项,系数化成1即可求解;
(2)去括号、移项、合并同类项,系数化成1即可求解;
(3)去括号、移项、合并同类项,系数化成1即可求解;
(4)去分母,去括号、移项、合并同类项,系数化成1即可求解;
(5)去分母,去括号、移项、合并同类项,系数化成1即可求解;
(6)去分母,去括号、移项、合并同类项,系数化成1即可求解.
解:(1)移项,得:0.5x+1.3x=6.5+0.7,
合并同类项,得:1.8x=7.2,
系数化为1得:x=4;
(2)去括号,得:1﹣4x﹣6=﹣6x﹣3,
移项,得﹣4x+6x=﹣3﹣1+6,
合并同类项,得2x=2,
系数化成1得:x=1;
(3)去括号,得5x+40=12x﹣42+5,
移项,得5x﹣12x=﹣42+5﹣40,
合并同类项,得﹣7x=﹣77,
系数化成1得x=11;
(4)去分母,得25﹣(x+1)=5x,
去括号,得25﹣x﹣1=5x,
移项,得﹣x﹣5x=1﹣25,
合并同类项,得:﹣6x=﹣24,
系数化成1得:x=4;
(5)去分母,得:3(x+2)﹣2(2x﹣3)=12,
去括号,得3x+6﹣4x+6=12,
移项,得3x﹣4x=12﹣6﹣6,
合并同类项,得﹣x=0,
系数化成1得:x=0;
(6)去分母,得:3(2x﹣1)﹣2(2x+5)=6x﹣7﹣6,
去括号,得:6x﹣3﹣4x﹣10=6x﹣7﹣6,
移项,得6x﹣4x﹣6x=﹣7﹣6+3+10,
合并同类项,得:﹣4x=0,
系数化成1得:x=0.


科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点 E、F 分别在边 BC、CD 上,且 BE=CF.连接 AE、BF.下列结论错误的是()

A. AE=BF B. AE⊥BF C. ∠DAE=∠BFC D. ∠AEB+∠BFC=1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要个小立方体,王亮所搭几何体的表面积为 . 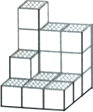
查看答案和解析>>
科目:初中数学 来源: 题型:
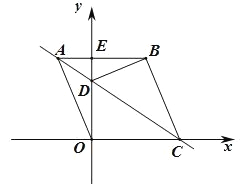
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD . 若B(1,0),则点C的坐标为( ) 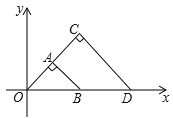
A.(1,2)
B.(1,1)
C.(- ![]() ,-
,- ![]() )
)
D.(2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC , AB=12,AC=15,D为AB上一点,且AD= ![]() AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( ) 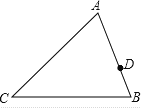
A.![]()
B.10
C.![]() 或10
或10
D.以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F= ![]() ,∠A=
,∠A= ![]() ,∠D=
,∠D= ![]()
B.∠C=∠F= ![]() ,AB=10,BC=6,DE=15,EF=9
,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F= ![]() ,
, ![]()
D.∠B=∠E= ![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com