
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD . 若B(1,0),则点C的坐标为( ) 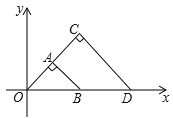
A.(1,2)
B.(1,1)
C.(- ![]() ,-
,- ![]() )
)
D.(2,1)
【答案】B
【解析】解答:∵∠OAB=∠OCD=90°,AO=AB , CO=CD , 等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0), ∴BO=1,则AO=AB= ![]() ,
,
∴A( ![]() ,
, ![]() ),
),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为(1,1).
故选:B.
分析:先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似求得答案.若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k , △ABC上一点的坐标是(x , y),则在△A′B′C′中,它的对应点的坐标是(kx , ky)或(-kx , ky).
【考点精析】本题主要考查了位似变换的相关知识点,需要掌握它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心)才能正确解答此题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.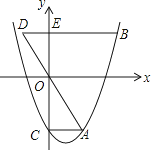
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列一元一次方程:
(1)0.5x﹣0.7=6.5﹣1.3x (2)1﹣2(2x+3)=﹣3(2x+1)
(3)5(x+8)=6(2x﹣7)+5; (4)5﹣![]() =x
=x
(5)![]() ﹣
﹣![]() =1 (6)
=1 (6)![]() ﹣
﹣![]() =
=![]() ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
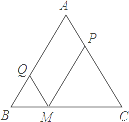
【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)
(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为__________.
(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由。
(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
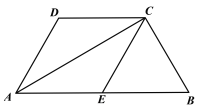
【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com