
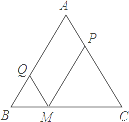
【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
【答案】(1)AB=QM+PM,证明见解析;(2)当M为底边BC的中点时,四边形AQMP为菱形,证明见解析;(3)当∠A=90°时, 菱形AQMP为正方形.
【解析】(1)根据平行四边形的判定得出平行四边形AQMP,求出BQ=MQ即可;
(2)求出AQ=QM,根据菱形的判定推出即可;
(3)根据有一个角是直角的菱形是正方形求解即可.
(1)AB=QM+PM
证明:∵PM‖AB,QM‖AC
∴四边形AQMP为平行四边形
∴PM=AQ
∵QM‖AC
∴∠C=∠QMB
∵AB=AC
∴∠C=∠B
∴∠B=∠QMB
∴BQ=MQ
∵AB=AQ+BQ
∴AB=QM+PM
(2)当M为底边BC的中点时,四边形AQMP为菱形
证明:连接AM

∵M为底边BC的中点,AB=AC
∴∠BAM=∠MAC
∵PM‖AB
∴∠BAM=∠AMP
∴∠MAC=∠AMP
∴PA=PM
∴平行四边形AQMP为菱形
(3)当∠A=90°时, 菱形AQMP为正方形
由(2)知,四边形AQMP为菱形,
∵∠A=90°,
∴菱形AQMP为正方形.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
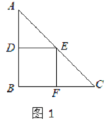
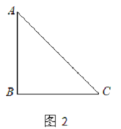
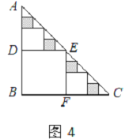
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
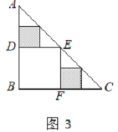
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
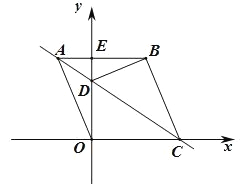
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别代表﹣40,20,两只电子蚂蚁甲,乙分别从AB两点同时出发,甲沿线段AB以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止,乙沿BA方向以5个单位长度/秒的速度向左运动.
![]()
(1)A,B两点间的距离为 个单位长度;甲到达B点时共运动了 秒.
(2)甲,乙在数轴上的哪个点相遇?
(3)多少秒时,甲、乙相距28个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD . 若B(1,0),则点C的坐标为( ) 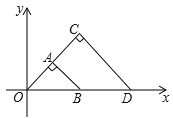
A.(1,2)
B.(1,1)
C.(- ![]() ,-
,- ![]() )
)
D.(2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在数轴上表示的数分别为a,b,且|a+6|+(b-18)2=0(规定:数轴上A,B两点之间的距离记为AB).
(1)求b-a的值.
(2)数轴上是否存在点C,使得CA=3CB?若存在,请求出点C所表示的数;若不存在,请说明理由.
(3)动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,且P比Q先运动2秒.问点Q运动多少秒时,P,Q相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域交流越来越深,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动.据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的![]() 还少25万件,求北京故宫博物院约有多少万件藏品?
还少25万件,求北京故宫博物院约有多少万件藏品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com