练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知反比例函数 的图象经过点M（2，1）
    （1）该函数的表达式
    （2）当2＜x＜4时，求y的取值范围（直接写出结果）.

    【答案】
    （1）

    y=


    （2）

    ＜y＜1


    【解析】用待定系数法把（2，1）代入反比例函数 中得k的值，从而得到解析式；由 得 ，再根据条件2＜x＜4得2＜ ＜4，最后解不等式即可．此题主要考查了待定系数法求反比例函数解析式，以及反比例函数的性质，正确确定函数解析式是解题的关键．
    【考点精析】根据题目的已知条件，利用反比例函数的性质的相关知识可以得到问题的答案，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y= x2﹣2x﹣6 与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点，点E在抛物线上，且横坐标为4 ，AE与y轴交F．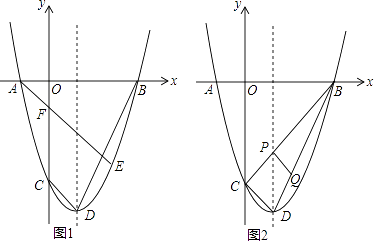

    （1）求抛物线的顶点D和F的坐标；
    （2）点M，N是抛物线对称轴上两点，且M（2 ，a），N（2 ，a+ ），是否存在a使F，C，M，N四点所围成的四边形周长最小，若存在，求出这个周长最小值，并求出a的值；
    （3）连接BC交对称轴于点P，点Q是线段BD上的一个动点，自点D以2 个单位每秒的速度向终点B运动，连接PQ，将△DPQ沿PQ翻折，点D的对应点为D′，设Q点的运动时间为t（0≤t≤ ）秒，求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的 时对应的t值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边三角形纸片ABC中，点D在边AB（不包含端点A、B）上运动，连接CD，将∠ADC对折，点A落在直线CD上的点A′处，得到折痕DE；将∠BDC对折，点B落在直线CD上的点B′处，得到折痕DF．

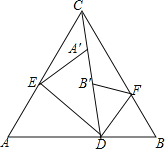
    （1）若∠ADC=80°，求∠BDF的度数；

    （2）试问∠EDF的大小是否会随着点D的运动而变化？若不变，求出∠EDF的大小；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在反比例函数 的图象的每一条曲线上，y都随x的增大而增大，则k的值可以是（　　）
    A.-1
    B.0
    C.1
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知CD=6m，AD=8m，∠ADC=90°，BC=24m，AB=26m．图中阴影部分的面积=_____m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，分别是两根木杆及其影子的图形．

    （1）哪个图形反应了阳光下的情形？哪个图反映了路灯下的情形？
    （2）请你画出图中表示小树影长的线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】莫小贝在襄阳北街租了一家商铺专门销售各种旅游纪念品.本月初他在进货时发现：若购进甲种纪念品 3

    件，乙种纪念品 2 件，需要 400 元，若购进甲种纪念品 4 件，乙种纪念品 5 件，需要 650 元. (1)求购进甲乙两种纪念品每件各需要多少元?

    (2)若莫小贝决定购进这两种纪念品共 100 件，其中甲种纪念品的数量不少于 65 件.考虑到资金周转，用于购 买这些纪念品的资金不超过 9000 元，那么莫小贝共有几种进货方案?

    (3)若每卖出一件甲种纪念品可获利润 20 元，一件乙种纪念品可获利润 35 元.在(2)的条件下，所购的 100 件 纪念品可以全部销售完，怎样进货才能使得获得的利润最大?最大利润是多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

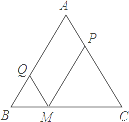
    【题目】已知：△ABC中AB=AC，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.

    探究:（1）线段QM、PM、AB之间有什么关系？并说明你的理由.

    （2）当M位于BC的什么位置时, 四边形AQMP是菱形？并说明你的理由.

    （3）当△ABC满足什么条件菱形AQMP是正方形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（　　）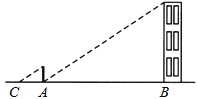
    A.10米
    B.12米
    C.15米
    D.22.5米

    查看答案和解析>>

    同步练习册答案