
【题目】如图,抛物线y= ![]() x2﹣2x﹣6
x2﹣2x﹣6 ![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4 ![]() ,AE与y轴交F.
,AE与y轴交F.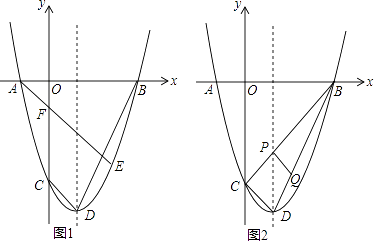
(1)求抛物线的顶点D和F的坐标;
(2)点M,N是抛物线对称轴上两点,且M(2 ![]() ,a),N(2
,a),N(2 ![]() ,a+
,a+ ![]() ),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
(3)连接BC交对称轴于点P,点Q是线段BD上的一个动点,自点D以2 ![]() 个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤
个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤ ![]() )秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的
)秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的 ![]() 时对应的t值.
时对应的t值.
【答案】
(1)
解:∵y= ![]() x2﹣2x﹣6
x2﹣2x﹣6 ![]() =
= ![]() (x﹣2
(x﹣2 ![]() )2﹣8
)2﹣8 ![]() ,
,
∴顶点D坐标(2 ![]() ,﹣8
,﹣8 ![]() ),
),
由题意E(4 ![]() ,﹣8
,﹣8 ![]() ),A(﹣2
),A(﹣2 ![]() ,0),B(6
,0),B(6 ![]() ,0),
,0),
设直线AE解析式为y=kx+b,则有 ![]() ,解得
,解得 ![]() ,
,
∴直线AE解析式为y=﹣x﹣2 ![]() ,
,
∴点F坐标(0,﹣2 ![]() )
)
(2)
解:如图1中,作点F关于对称轴的对称点F′,连接FF′交对称轴于G,在CF上取一点C′,使得CC′= ![]() ,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.
,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.
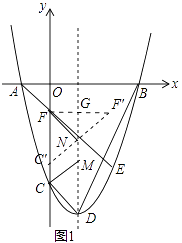
∵四边形CMNF的周长=CF+NM+CM+FN=5 ![]() +CM+NF,CM+NF=C′N+NF=C′N+NF′=C′F′(两点之间线段最短),
+CM+NF,CM+NF=C′N+NF=C′N+NF′=C′F′(两点之间线段最短),
∴此时四边形CMNF的周长最小.
∵C′F=3 ![]()
∴GN= ![]() C′F=
C′F= ![]() ,
,
∴﹣(a+ ![]() )=2
)=2 ![]() +
+ ![]()
![]() ,
,
∴a=﹣ ![]() ,
,
∵C′F′= ![]() =5
=5 ![]() ,
,
∴四边形CMNF的周长最小值=5 ![]() +5
+5 ![]() =10
=10 ![]()
(3)
解:如图2中,作PF⊥BD于F,QH⊥对称轴于H.
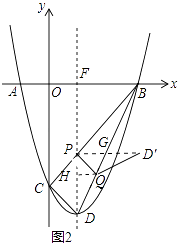
由题意可知BD= ![]() =4
=4 ![]() ,DQ=2
,DQ=2 ![]() t,
t,
∵S△PQG= ![]() S△DPQ=
S△DPQ= ![]() S△PD′Q,
S△PD′Q,
∴PG= ![]() PD′=
PD′= ![]() PD=2
PD=2 ![]() =
= ![]() BF,
BF,
情形①PG∥FB时,∵PF=PD,
∴BG=GD,
∴PG= ![]() BF=2
BF=2 ![]() ,
,
在Rt△QHD中,sin∠HDQ= ![]() ,DQ=2
,DQ=2 ![]() t,
t,
∴HQ=2 ![]() t,HD=4
t,HD=4 ![]() t,
t,
∵∠QPD′=∠QPD=45°,
∴PH=HQ=2 ![]() t,
t,
∴PH+HD=PD,
∴6 ![]() t=4
t=4 ![]() ,
,
∴t= ![]() .
.
情形②如图3中,PG′=PG=2 ![]() ,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.
,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.
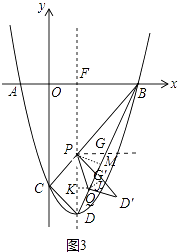
由sin∠PDG=sin∠GPM= ![]() =
= ![]() ,
,
∴MG′=MG= ![]() ,
,
∴G′D=BD﹣GG′= ![]() ,
,
∵ ![]() =
= ![]() =
= 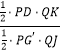 ,
,
∵∠QPD=∠QPG′,QK⊥PD,QJ⊥PG′,
∴QK=QJ,
∴ ![]() =
= ![]() =2,
=2,
∴QD= ![]() ×
× ![]() =
= ![]() ,
,
∴t= ![]() =
= ![]() ,
,
综上所述t= ![]() 或
或 ![]() 秒时,△D′PQ与△PQB重叠部分的面积为△DPQ面积的
秒时,△D′PQ与△PQB重叠部分的面积为△DPQ面积的 ![]()
【解析】(1)利用配方法或公式法求顶点坐标,求出最小AE即可求出点F坐标.(2)如图1中,作点F关于对称轴的对称点F′,连接FF′交对称轴于G,在CF上取一点C′,使得CC′= ![]() ,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.(3)分两种情形①PG∥FB时;②如图3中,PG′=PG=2
,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.(3)分两种情形①PG∥FB时;②如图3中,PG′=PG=2 ![]() ,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.分别求解即可.
,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.分别求解即可.
【考点精析】通过灵活运用二次函数的图象,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF,CF. 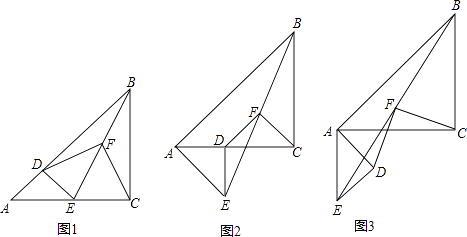
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系(不用证明); 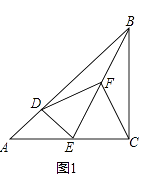
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断; 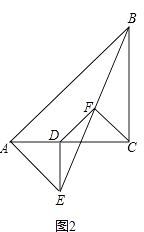
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). 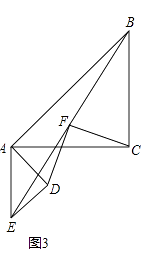
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
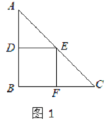
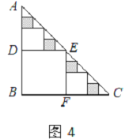
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
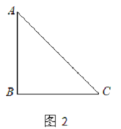
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
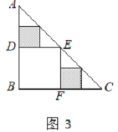
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com