【题目】如图，已知CD=6m，AD=8m，∠ADC=90°，BC=24m，AB=26m．图中阴影部分的面积=_____m2．
【答案】96
【解析】
利用勾股定理求出AC值，结合三角形面积公式求得S△ADC；
接下来计算AC2+BC2、AB2，可得△ABC为直角三角形，结合三角形面积公式求得S△ABC，然后根据阴影部分的面积=S△ABC-S△ADC计算即可.
∵CD=6m，AD=8m，∠ACD=90°，
∴AC=10m，S△ADC=
×6×8=24（m2）.
∵AC=10m，CB=24m，AB=26m，
∴AC2+BC2=AB2，
∴△ABC是以AB为斜边的直角三角形.
∵△ABC是直角三角形，AC=10m，CB=24m，
∴S△ABC=×10×24=120（m2），
∴S△ABC-S△ADC=120-24=96（m2）.
即图中阴影部分的面积为96m2.
故答案为：96.
科目：初中数学 来源： 题型：
【题目】已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连接DF，CF．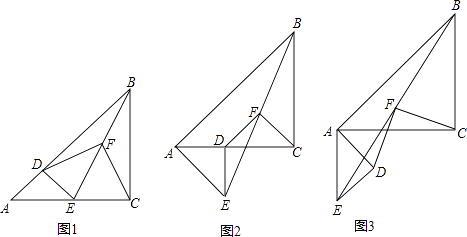 
（1）如图1，当点D在AB上，点E在AC上，请直接写出此时线段DF，CF的数量关系和位置关系（不用证明）；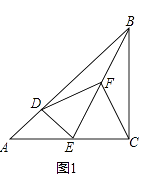 
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；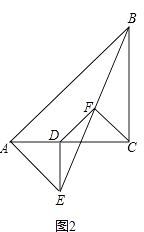 
（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC= 
，求此时线段CF的长（直接写出结果）． 
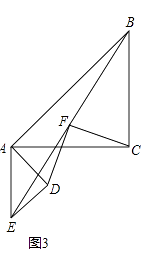
查看答案和解析>>
科目：初中数学 来源： 题型：
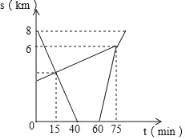
【题目】小刘从家里骑自行车出发，去镇上超市途中碰到妹妹甜甜走路从镇上回家，小刘在超市买完东西回家，在回去的路上又碰到了甜甜，便载甜甜一起回家，结果小刘比正常速度回家的时间晚了3分钟，二人离镇的距离S（千米）和小刘从家出发后的时间t（分钟）之间的关系如图所示，（假设二人之间交流时间忽略不计）
（1）小刘家离镇上的距离 ．
（2）小刘和甜甜第1次相遇时离镇上距离是多少？
（3）小刘从家里出发到回家所用的时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是以BC为底的等腰三角形，AD是边BC上的高，点E、F分别是AB、AC的中点．
（1）求证：四边形AEDF是菱形；
（2）如果四边形AEDF的周长为12，两条对角线的和等于7，求四边形AEDF的面积S．
查看答案和解析>>
科目：初中数学 来源： 题型：
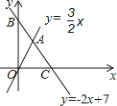
【题目】如图，直线
与
轴、
轴分别相交于点C、B，与直线
相交于点A．
（1）求A点坐标；
（2）如果在y轴上存在一点P，使△OAP是以OA为底边的等腰三角形，求P点坐标；
（3）在直线上是否存在点Q，使△OAQ的面积等于6？若存在，请求出Q点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了从甲乙两人中选拔一人参加初中数学竞赛，每个月对他们进行一次测试，如图绘出了两个人赛前 5 次测验成绩(每次测验成绩都是 5 的倍数).
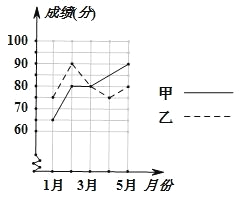
(1)分别求出甲乙两人 5 次测验成绩的平均数与方差；
(2)如果你是他们的辅导老师，应该选拔哪位学生参加这次竞赛，并简要说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知数轴上有A，B两点，分别代表﹣40，20，两只电子蚂蚁甲，乙分别从AB两点同时出发，甲沿线段AB以3个单位长度/秒的速度向右运动，甲到达点B处时运动停止，乙沿BA方向以5个单位长度/秒的速度向左运动．
（1）A，B两点间的距离为 个单位长度；甲到达B点时共运动了 秒．
（2）甲，乙在数轴上的哪个点相遇？
（3）多少秒时，甲、乙相距28个单位长度？
（4）若乙到达A点后立刻掉头并保持速度不变，则甲到达B点前，甲，乙还能在数轴上相遇吗？若能，求出相遇点所对应的数；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数y＝
x－15的图象与x轴，y轴分别交于点A，B，O为坐标原点，则在△OAB内部(包括边界)，纵坐标、横坐标都是整数的点(整点)共有_________个．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
