
【题目】已知数轴上有A,B两点,分别代表﹣40,20,两只电子蚂蚁甲,乙分别从AB两点同时出发,甲沿线段AB以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止,乙沿BA方向以5个单位长度/秒的速度向左运动.
![]()
(1)A,B两点间的距离为 个单位长度;甲到达B点时共运动了 秒.
(2)甲,乙在数轴上的哪个点相遇?
(3)多少秒时,甲、乙相距28个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
【答案】(1)60,20;(2)![]() ;(3) 4秒或11秒时,甲、乙相距28个单位长度;(4)不能.
;(3) 4秒或11秒时,甲、乙相距28个单位长度;(4)不能.
【解析】
(1)根据A,B两点之间的距离AB=|﹣40﹣20|,根据题意即可求解;
(2)根据题意列方程即可得到结论;
(3)根据题意列方程即可得到结论;
(4)设甲到达B点前,甲,乙经过a秒在数轴上相遇,根据题意得方程解方程即可.
解:(1)A、B两点的距离为AB=|﹣40﹣20|=60,甲到达B点时共运动了60÷3=20秒;
故答案为:60,20;
(2)设它们按上述方式运动,甲,乙经过x秒会相遇,根据题意得
3x+5x=60,
解得 x=![]() ,
,
![]()
答:甲,乙在数轴上的![]() 点相遇;
点相遇;
(3)两种情况,相遇前,
设y秒时,甲、乙相距28个单位长度,根据题意得,3y+5y=60﹣28,
解得:y=4,
第一次相遇后,
设y秒时,甲、乙相距28个单位长度,根据题意得,
5y+3y﹣60=28,
解得:y=11,
答:4秒或11秒时,甲、乙相距28个单位长度;
(4)甲到达B点前,甲,乙不能在数轴上相遇,
理由:设甲到达B点前,甲,乙经过a秒在数轴上相遇,
根据题意得,3a+60=5a,
解得:a=30,
3a=3×30=90>60,
故甲,乙不能在数轴上相遇.


科目:初中数学 来源: 题型:
【题目】莫小贝在襄阳北街租了一家商铺专门销售各种旅游纪念品.本月初他在进货时发现:若购进甲种纪念品 3
件,乙种纪念品 2 件,需要 400 元,若购进甲种纪念品 4 件,乙种纪念品 5 件,需要 650 元. (1)求购进甲乙两种纪念品每件各需要多少元?
(2)若莫小贝决定购进这两种纪念品共 100 件,其中甲种纪念品的数量不少于 65 件.考虑到资金周转,用于购 买这些纪念品的资金不超过 9000 元,那么莫小贝共有几种进货方案?
(3)若每卖出一件甲种纪念品可获利润 20 元,一件乙种纪念品可获利润 35 元.在(2)的条件下,所购的 100 件 纪念品可以全部销售完,怎样进货才能使得获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
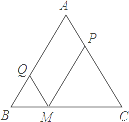
【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
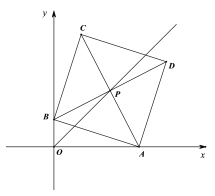
【题目】在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
(1)如果∠BAO=45°,直接写出点P的坐标;
(2)求证:点P在∠AOB的平分线上;
(3)设点P到x轴的距离为h,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名八年级学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图均不完整),请根据图中所给信息解答下列问题:
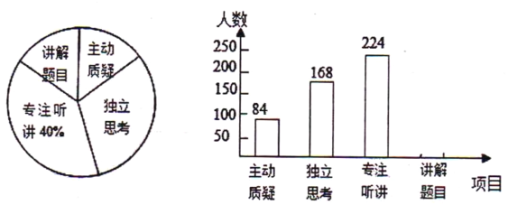
(1)在这次评价中,一共抽查了多少名学生?
(2)求扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com