
【题目】等腰△ABC中,AB=AC=5,△ABC的面积为10,则BC=_____.
【答案】2![]() 或4
或4![]() .
.
【解析】
作CD⊥AB于D,则∠ADC=∠BDC=90°,由三角形的面积求出CD,由勾股定理求出AD;分两种情况:①等腰△ABC为锐角三角形时,求出BD,由勾股定理求出BC即可;②等腰△ABC为钝角三角形时,求出BD,由勾股定理求出BC即可.
作CD⊥AB于D,则∠ADC=∠BDC=90°,△ABC的面积=![]() ABCD=
ABCD=![]() ×5×CD=10,解得:CD=4,∴AD=
×5×CD=10,解得:CD=4,∴AD=![]() =
=![]() =3;
=3;
分两种情况:
①等腰△ABC为锐角三角形时,如图1所示:
BD=AB﹣AD=2,∴BC=![]() =
=![]() =2
=2![]() ;
;
②等腰△ABC为钝角三角形时,如图2所示:
BD=AB+AD=8,∴BD=![]() =
=![]() =4
=4![]() ;
;
综上所述:BC的长为2![]() 或4
或4![]() .
.
故答案为:2![]() 或4
或4![]() .
.


科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF,CF. 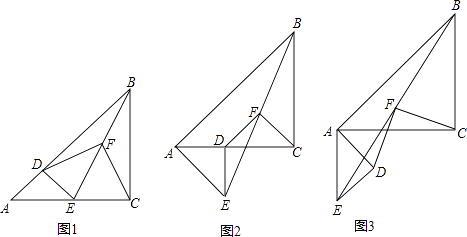
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系(不用证明); 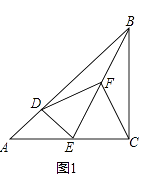
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断; 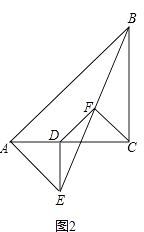
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). 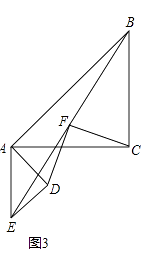
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
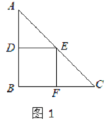
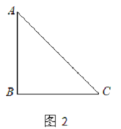
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
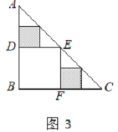
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
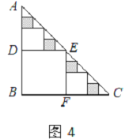
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
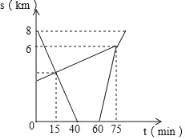
【题目】小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)
(1)小刘家离镇上的距离 .
(2)小刘和甜甜第1次相遇时离镇上距离是多少?
(3)小刘从家里出发到回家所用的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别代表﹣40,20,两只电子蚂蚁甲,乙分别从AB两点同时出发,甲沿线段AB以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止,乙沿BA方向以5个单位长度/秒的速度向左运动.
![]()
(1)A,B两点间的距离为 个单位长度;甲到达B点时共运动了 秒.
(2)甲,乙在数轴上的哪个点相遇?
(3)多少秒时,甲、乙相距28个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com