
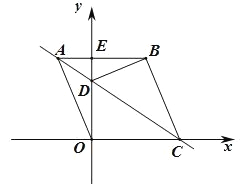
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
【答案】(1)菱形 ABCO 的边长为 13;(2) BD 所在直线为![]() ;(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为
;(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为![]() 或
或![]() .
.
【解析】
(1)在Rt△AOE中利用勾股定理即可求得菱形的边长;
(2)根据(1)即可求的OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式,求出点D的坐标,再利用待定系数法求BD的解析式即可;
(3)设点P(a,![]() ),根据S△PBD =
),根据S△PBD =![]() =S△EBD列式计算即可.
=S△EBD列式计算即可.
(1)∵四边形 ABCO 为菱形,
∴AB∥CO,
∴∠AEO=∠EOC=90°,
∴在 Rt△EHD 中,
![]() ,
,
∴菱形 ABCO 的边长为 13;
(2)∵四边形 ABCO 为菱形
∴OC=OA=AB=13,
∴BE=AB-AE=13-5=8,
∴点 B 坐标为(8,12),点 C 的坐标为(13,0), 设 AC 所在直线为 y=kx+b,
根据题意得![]() ,
,
解得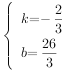 ,
,
![]() ,
,
∴AC 所在直线为![]() ,
,
∴当 x=0 时,
∴点 D 的坐标为![]() ,
,
同上理可得 BD 所在直线为![]() ;
;
(3)存在点 P 使得△PBD 与△EBD 的面积相等, 点 P 的坐标为![]() 或
或![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
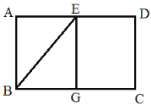
【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
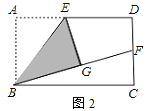
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
![]() 求证:BF=AB+DF;
求证:BF=AB+DF;
![]() 若AD=
若AD=![]() AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莫小贝在襄阳北街租了一家商铺专门销售各种旅游纪念品.本月初他在进货时发现:若购进甲种纪念品 3
件,乙种纪念品 2 件,需要 400 元,若购进甲种纪念品 4 件,乙种纪念品 5 件,需要 650 元. (1)求购进甲乙两种纪念品每件各需要多少元?
(2)若莫小贝决定购进这两种纪念品共 100 件,其中甲种纪念品的数量不少于 65 件.考虑到资金周转,用于购 买这些纪念品的资金不超过 9000 元,那么莫小贝共有几种进货方案?
(3)若每卖出一件甲种纪念品可获利润 20 元,一件乙种纪念品可获利润 35 元.在(2)的条件下,所购的 100 件 纪念品可以全部销售完,怎样进货才能使得获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列一元一次方程:
(1)0.5x﹣0.7=6.5﹣1.3x (2)1﹣2(2x+3)=﹣3(2x+1)
(3)5(x+8)=6(2x﹣7)+5; (4)5﹣![]() =x
=x
(5)![]() ﹣
﹣![]() =1 (6)
=1 (6)![]() ﹣
﹣![]() =
=![]() ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
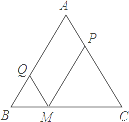
【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
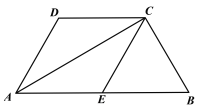
【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( ) 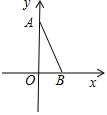
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com