
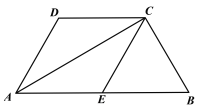
【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
【答案】(1)见解析;(2)![]()
【解析】(1)先证AE=CD,AE∥CD,得四边形AECD是平行四边形,再证CE=AE ,得
平行四边形AECD是菱形;
(2)过点C作CF⊥EB交EB于点F. 先求EF,再根据勾股定理求CF,再根据平行四边形面积公式可求出四边形面积.
(1)∵E为AB的中点
∴AB=2AE
∵AB=2CD
∴AE=CD
又∵AB∥CD
∴AE∥CD
∴四边形AECD是平行四边形
∵AC⊥BC
∴∠ACB=90°
又∵E为AB的中点
∴![]() ,
,![]()
∴CE=AE
平行四边形AECD是菱形
(2)过点C作CF⊥EB交EB于点F.
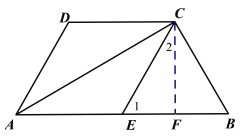
∵四边形AECD是菱形
∴AD∥EC,AE=CE
∴∠DAE=∠1
∵∠DAE=60°,AE=2
∴∠1=60°,CE=2
∵CF⊥EB
∴∠CFE=90°
∴∠1+∠2=90°
∴∠2=30°
∴![]()
![]() ,
,![]()
∴![]()


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
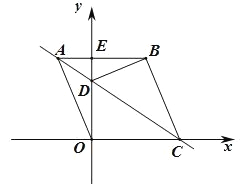
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD . 若B(1,0),则点C的坐标为( ) 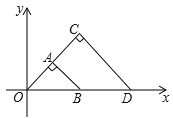
A.(1,2)
B.(1,1)
C.(- ![]() ,-
,- ![]() )
)
D.(2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在数轴上表示的数分别为a,b,且|a+6|+(b-18)2=0(规定:数轴上A,B两点之间的距离记为AB).
(1)求b-a的值.
(2)数轴上是否存在点C,使得CA=3CB?若存在,请求出点C所表示的数;若不存在,请说明理由.
(3)动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,且P比Q先运动2秒.问点Q运动多少秒时,P,Q相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC , AB=12,AC=15,D为AB上一点,且AD= ![]() AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( ) 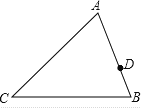
A.![]()
B.10
C.![]() 或10
或10
D.以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域交流越来越深,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动.据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的![]() 还少25万件,求北京故宫博物院约有多少万件藏品?
还少25万件,求北京故宫博物院约有多少万件藏品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组的小明想测量教学楼前的一棵树的高度.下午课外活动时他测得一根长为1m的竹竿的影长是0.8m.但当他马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图).他先测得留在墙壁上的树影高为1.2m,又测得地面的影长为2.6m,请你帮他算一下,下列哪个数字最接近树高( )m. 
A.3.04
B.4.45
C.4.75
D.3.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,

(1)按此规律,图案⑦需____根火柴棒;第n个图案需____根火柴棒.
(2)用2018根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com