
【题目】如图,正方形ABCD中,点 E、F 分别在边 BC、CD 上,且 BE=CF.连接 AE、BF.下列结论错误的是()

A. AE=BF B. AE⊥BF C. ∠DAE=∠BFC D. ∠AEB+∠BFC=1200
【答案】D
【解析】根据正方形的性质可以证明△ABE≌△BCF,可以得出AE=BF,∠BAE=∠CBF,再由直角三角形的性质就可以得出∠BGE=90°,由∠BAE+∠AEB=90°,∠CBF+∠AEB=90°可得∠DAE=∠BFC,无法说明∠AEB+∠BFC=120°.
A.∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠BCD=90°.
在△ABE与△BCF中
AB=BC,∠ABE=∠BCF,BE=CF
∴△ABE≌△BCF(SAS)
∴AE=BF;
故A正确;
(2)由△ABE≌△BCF
∴∠BAE=∠CBF.
∵∠ABE=90°
∴∠BAE+∠AEB=90°
∴∠CBF+∠AEB=90°
∴∠BGE=90°
∴AE⊥BF.
故B正确;
C. ∵∠BAE=∠CBF,
∠BAE+∠AEB=90°,∠CBF+∠AEB=90°,
∴∠DAE=∠BFC,
故C正确;
D.无法说明∠AEB+∠BFC=120°,故D不正确;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.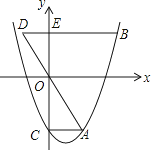
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,下列结论中,不正确的是( )
,下列结论中,不正确的是( )
A.图象必经过点(1,2)
B.y随x的增大而增大
C.图象在第一、三象限内
D.若x>1,则0<y<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列一元一次方程:
(1)0.5x﹣0.7=6.5﹣1.3x (2)1﹣2(2x+3)=﹣3(2x+1)
(3)5(x+8)=6(2x﹣7)+5; (4)5﹣![]() =x
=x
(5)![]() ﹣
﹣![]() =1 (6)
=1 (6)![]() ﹣
﹣![]() =
=![]() ﹣1.
﹣1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com