
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.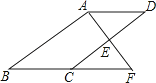
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
 ,
,
∴△ADE≌△FCE(AAS)
(2)
解:∵ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在ABCD中,AD=BC=5,
∴DE= ![]() =
= ![]() =4,
=4,
∴CD=2DE=8
【解析】(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;
(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.此题考查了平行四边形的性质、全等三角形的判定方法、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
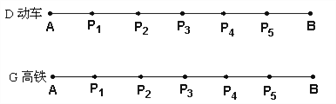
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

(1)根据车票中的信息填空:该列动车和高铁是__________向而行(填“相”或“同”).
(2)已知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A、B、C在数轴上对应的数分别为a、b、c满足|a+5|+|b-1|+|c-2|=0.
(1)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,请说明理由;
(2)若点A,B,C同时开始在数轴上分别以每秒1个单位长度,每秒3个单位长度,每秒5个单位长度沿着数轴负方向运动.经过t(t≥1)秒后,试问AB-BC的值是否会随着时间t的变化而变化?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要个小立方体,王亮所搭几何体的表面积为 . 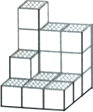
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com