
����Ŀ�����������Ų�ͬ���ͻij�Ʊ����![]() ������ʾ��������
������ʾ��������![]() ������ʾ��������
������ʾ��������

��1�����ݳ�Ʊ�е���Ϣ��գ����ж���������__________����У�������������ͬ������
��2����֪���ж���������ƽ���ٶȷֱ�Ϊ![]() ��
��![]() �����лij��Ȳ��ƣ�
�����лij��Ȳ��ƣ�
�پ������㣬������л�ֱ���յ㣨����;����ͣ���κ�վ�㣩�������ȶ������絽![]() ����
����![]() ��
��![]() ����֮��ľ��룮
����֮��ľ��룮
���ڢ��в�������ݻ����ϣ���֪![]() ��
��![]() ����;����������
����;����������![]() ��վ��
��վ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ������ÿ��վ�㶼ͣ��������ֻͣ��
������ÿ��վ�㶼ͣ��������ֻͣ��![]() ��
��![]() ����վ�㣬���л���ÿ��ͣ��վ�㶼ͣ��
����վ�㣬���л���ÿ��ͣ��վ�㶼ͣ��![]() ������и����϶�����ʱ�̣�
������и����϶�����ʱ�̣�
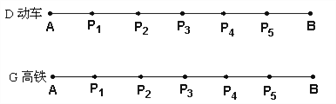
���𰸡���1��ͬ����2����1200km����8��55��.
�������������������1���ɳ�Ʊ���Եó���������������A�ؿ���B�أ����Զ���������ͬ����У���2�������ȶ���������1��Сʱ�����Զ����ȸ���ȫ�̶��2��Сʱ����A��B���ؾ���Ϊxkm������з���![]() ��
��![]() =2�����x��������3��ÿ������վ�����Ϊ��1200��6=200km��
=2�����x��������3��ÿ������վ�����Ϊ��1200��6=200km��
������ÿվ����ʱ��Ϊ��200��300=![]() h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
��������������ÿһվ��ʱ��ͼ���ɴ˿��Եó�������P2��P3֮���ϲ��������������������yСʱ���϶�������y��![]() ����300=��y+1��
����300=��y+1��![]() ��2����200�����y=
��2����200�����y=![]() .
.
���Ը����ھ���![]() h������϶������ϵ�ʱ��Ϊ8��55��.
h������϶������ϵ�ʱ��Ϊ8��55��.
���������
��1��ͬ��
��2������A��B���ؾ���Ϊxkm����
![]() ��
��![]() =2�����x=1200��
=2�����x=1200��
����A��B����֮��ľ���Ϊ1200km��
��ÿ������վ�����Ϊ��1200��6=200km��
������ÿվ����ʱ��Ϊ��200��300=![]() h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
���Զ���������ÿһվ��ʱ����ͼ��ʾ��

�ɴ˿��Եó�������P2��P3֮���ϲ�����������
���������yСʱ���϶�����
����y��![]() ����300=��y+1��
����300=��y+1��![]() ��2����200�����y=
��2����200�����y=![]() .
.
���Ը����ھ���![]() h������϶������ϵ�ʱ��Ϊ8��55��.
h������϶������ϵ�ʱ��Ϊ8��55��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��
��1��4x��5=3x+2
��2��![]()
��3��2x��3��6��x��=3x��4��5��x��
��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
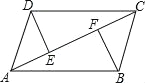
����Ŀ����֪DE��AC��BF��AC������ֱ���E��F��AE=CF��DC��AB��
��1����֤����DE=BF��
��2������DF��BE������DF��BE�Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=4��BC=2��P��AB����һ���㣬PD��AC�ڵ�D����E��P���Ҳ࣬��PE=1������CE��P�ӵ�A��������AB�����˶�����E�����Bʱ��Pֹͣ�˶����������˶������У�ͼ����Ӱ�������S1+S2�Ĵ�С�仯����ǣ� �� 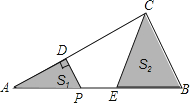
A.һֱ��С
B.һֱ����
C.�ȼ�С������
D.��������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��ABCD�ı�CD���е㣬�ӳ�AE��BC���ӳ����ڵ�F��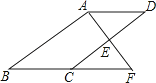
��1����֤����ADE�ա�FCE��
��2������BAF=90�㣬BC=5��EF=3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=15��AC=13��BC���ϵĸ�AD=12����BC�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
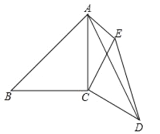
����Ŀ����ͼ����֪��ACB=��DCE=90�㣬AC=BC��AB=![]() ��CE=CD��AE=2����CAE=45�㣬��AD�ij���
��CE=CD��AE=2����CAE=45�㣬��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ����AOC����BOD�й�������O�����н��ۣ�
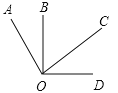
�١�AOB=��COD��
�ڡ�AOB+��COD=![]() ��
��
����OBƽ����AOC����OCƽ����BOD��
�ܡ�AOD��ƽ��������BOC��ƽ������ͬһ��������
������ȷ���� �����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݹ��ҷ���ίʵʩ�����ݵ�������й��ļ�Ҫ��ij�н�ϵط�ʵ�ʣ�������2015��5��1����Ծ��������õ�ʵʩ�����ݵ�����շѣ������շѱ����±���
һ������һ�����õ����ķ�Χ ��Ѽ۸�λ��Ԫ/ǧ��ʱ��
������150ǧ��ʱ�IJ��� a
����150ǧ��ʱ����������300ǧ��ʱ�IJ��� b
����300ǧ��ʱ�IJ��� a+0.3
2015��5�·ݣ����о�����õ�100ǧ��ʱ������60Ԫ���������õ�200ǧ��ʱ������122.5Ԫ��
��1�����ϱ���a��b��ֵ��
��2��ʵʩ�����ݵ�����շ��Ժ���һ���������õ����ǧ��ʱ���䵱�½���277.5Ԫ��
��3��ʵʩ�����ݵ�����շ��Ժ���һ���������õ����ǧ��ʱ���䵱�µ�ƽ����۵���0.62Ԫ/ǧ��ʱ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com