
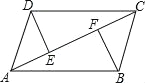
【题目】已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
(1)试证明:DE=BF;
(2)连接DF、BE,猜想DF与BE的关系?
【答案】见解析
【解析】(1)求出AF=CE,∠AFB=∠DEC=90°,根据平行线的性质得出∠DCE=∠BAF,根据ASA推出△AFB≌△CED即可;
(2)(2)根据平行四边形的判定得出四边形DEBF是平行四边形,再根据平行四边形的性质得出即可.
(1)证明:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠DEC=90°,
∵DC∥AB,
∴∠DCE=∠BAF,
在△AFB和△CED中
∴△AFB≌△CED,
∴DE=BF;
(2)如图所示:
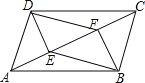
猜想:DF=BE,DF∥BE,
证明:∵DE⊥AC,BF⊥AC,
∴DE∥BF,
∵DE=BF,
∴四边形DEBF是平行四边形,
∴DF=BE,DF∥BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
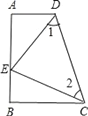
【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.
(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)你认为“AD→DB”是最短路线吗?如果你认为不是,请计算出最短的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程:①3x﹣1=2x+1,②![]() ,③
,③![]() ,④
,④![]() x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )
A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
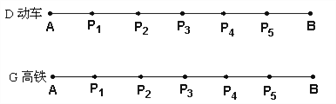
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

(1)根据车票中的信息填空:该列动车和高铁是__________向而行(填“相”或“同”).
(2)已知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A地将一批物品运往B地,再返回A地,图6表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:
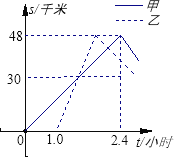
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com