
【题目】如图,点E在线段CD上,AE,BE分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC有怎样的位置关系?并说明理由.

【答案】(1) AD=3,BC=4;(2)AD∥BC.理由见解析.
【解析】
(1)根据题意可知x-3=0,y-4=0,易求解AD和BC的长;(2)根据∠AEB=90°,可得∠EAB+∠EBA=90°,因为EA、EB分别平分∠DAB和∠CBA,则∠DAB+∠ABC=180°,所以AD∥BC.
(1)∵(x-3)2+|y-4|=0,
∴x-3=0,y-4=0,解得x=3,y=4.
∴AD=3,BC=4.
(2)AD∥BC.
理由:∵AE,BE分别平分∠DAB和∠CBA,
∴∠DAE=∠EAB,∠CBE=∠EBA.
∵∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠DAE+∠CBE=90°,
∴∠EAB+∠EBA+∠DAE+∠CBE=180°,
即∠DAB+∠CBA=180°,∴AD∥BC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两种型号的风扇成本分别为120元台、170元台,销售情况如下表所示(成本、售价均保持不变,利润=收入-成本):
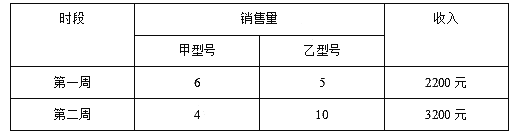
(1)求这两种型号风扇的售价;
(2)该商场打算再采购这两种型号的风扇共130台,销售完后总利润能不能恰好为8010元?若能,给出相应的采购方案;若不能,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB ,分别交AB、BC于点D 、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.
(1)如图1,若∠BAC= 100°,求∠EAN的度数;
(2)如图2,若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=a(a≠90°),请直接写出∠EAN的度数. (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
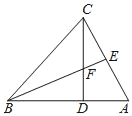
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE与BD交于点A.求证:
(1)BF=AC;
(2)BE是AC的中垂线;
(3)若AD=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理:

∵∠1=∠2(已知),
∴________∥________(__________________________).
∵∠2=∠3(已知),
∴________∥________(___________________________),
∴________∥________(___________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )
A.41
B.40
C.39
D.38
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.
(1)如图1,当点A的横坐标为时,矩形AOBC是正方形;
(2)如图2,当点A的横坐标为- ![]() 时,
时,
①求点B的坐标;
②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=﹣x2 , 试判断抛物线y=﹣x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com