
【题目】在△ABC中,DE垂直平分AB ,分别交AB、BC于点D 、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.
(1)如图1,若∠BAC= 100°,求∠EAN的度数;
(2)如图2,若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=a(a≠90°),请直接写出∠EAN的度数. (用含a的代数式表示)

【答案】(1)∠EAN=20°;(2)∠EAN=40°;(3)当0<a<90°时,∠EAN=180°-2a;当180°>a>90°时,∠EAN=2a -180°.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据∠EAN=∠BAC-(∠BAE+∠CAN)代入数据进行计算即可得解;
(2)同(1)的思路,最后根据∠EAN=∠BAE+∠CAN-∠BAC代入数据进行计算即可得解;
(3)根据前两问的求解,分α<90°与α>90°两种情况解答.
(1)因为DE垂直平分AB,
所以AE=BE,∠BAE=∠B,
同理可得∠CAN= ∠C,
所以∠EAN=∠BAC -∠BAE-∠CAN=∠BAC -(∠B+∠C),
在△ABC中,∠B+∠C=180°- ∠BAC=80°,
所以∠EAN= 100-80=20°;
(2)因为 DE垂直平分AB,
所以AE= BE,∠BAE=∠B,
同理可得∠CAN= ∠C,
所以∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C= 180°-∠BAC= 110°,
所以∠EAN=110°- 70°=40°;
(3)当0<a<90°时,∠EAN=180°-2a;
当180°>a>90°时,∠EAN=2a -180°.


科目:初中数学 来源: 题型:
【题目】把抛物线y=﹣ ![]() 经( )平移得到y=﹣
经( )平移得到y=﹣ ![]() ﹣1.
﹣1.
A.向右平移2个单位,向上平移1个单位
B.向右平移2个单位,向下平移1个单位
C.向左平移2个单位,向上平移1个单位
D.向左平移2个单位,向下平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图中,每个正方形由边长为1的小正方形组成: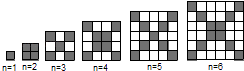
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
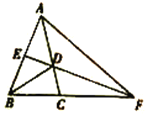
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生去福利院献爱心,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)向甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2400元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
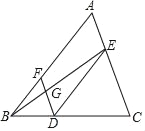
【题目】完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在线段CD上,AE,BE分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC有怎样的位置关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA= ![]() ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com