练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m．其行走路线如图所示，第1次移动到A1，第2次移动到A2，…，第n次移动到An．则△OA2A2018的面积是（　　）

    A. 504m2 B. m2 C. m2 D. 1009m2

    【答案】A

    【解析】

    由OA4n=2n知OA2017=+1=1009，据此得出A2A2018=1009-1=1008，据此利用三角形的面积公式计算可得．

    由题意知OA4n=2n，

    ∴OA2016=2016÷2=1008，即A2016坐标为(1008，0)，

    ∴A2018坐标为(1009，1)，

    则A2A2018=1009－1=1008(m)，

    ∴＝A2A2018×A1A2＝×1008×1＝504(m2).

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

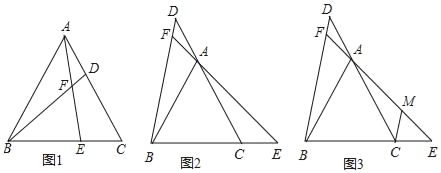
    【题目】已知△ABC是等边三角形，在直线AC、直线BC上分别取点D和点且AD=CE，直线BD、AE相交于点F．

    （1）如图1所示，当点D、点E分别在线段CA、BC上时，求证：BD=AE；

    （2）如图2所示，当点D、点E分别在CA、BC的延长线时，求∠BFE的度数；

    （3）如图3所示，在（2）的条件下，过点C作CM∥BD，交EF于点M，若DF：AF：AM=1：2：4，BC=12，求CE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一组数据1，2，3，4，x的平均数与中位数相同，则实数x的值不可能是( )

    A. 0 B. 2.5 C. 3 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的方格中，每个小方格都是边长为1个单位长度的正方形，的三个顶点都在格点（小方格的顶点）上．

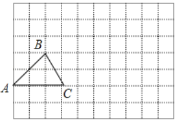
    （1）请建立适当的平面直角坐标系，使，，并写出点的坐标；

    （2）在（1）的条件下，将先向右平移4个单位长度再向上平移2个单位长度后可得到，请在图中画出平移后的，并分别写出点，，的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】雷达二维平面定位的主要原理是：测量目标的两个信息―距离和角度，目标的表示方法为，其中，m表示目标与探测器的距离；表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为，目标C的位置表示为．用这种方法表示目标B的位置，正确的是（ ）

    A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两种型号的风扇成本分别为120元台、170元台,销售情况如下表所示(成本、售价均保持不变,利润=收入-成本)：

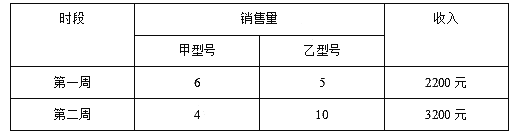
    (1)求这两种型号风扇的售价；

    (2)该商场打算再采购这两种型号的风扇共130台，销售完后总利润能不能恰好为8010元?若能，给出相应的采购方案；若不能，说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

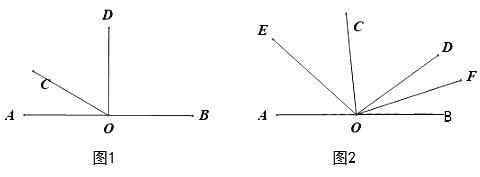
    【题目】如图1,点O是直线AB上的一点.

    (1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数；

    (2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2，OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小；若改变,说明理由；

    (3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD，多少秒时∠COM=∠BON(直接写出答案,不必写出过程).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是射线BM上的一个动点(点P不与点B重合)，∠AOB= 30°，∠ABM=60°.当∠OAP=______时，以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

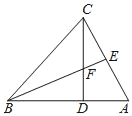
    【题目】如图，在△CBD中，CD=BD，CD⊥BD，BE平分∠CBA交CD于点F，CE⊥BE垂足是E，CE与BD交于点A．求证：

    （1）BF=AC；

    （2）BE是AC的中垂线；

    （3）若AD=2，求AB的长．

    查看答案和解析>>

    同步练习册答案