
【题目】如图,⊙O的半径为6,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC与∠BOC互补,则线段BC的长为( )
A.![]()
B.3
C.![]()
D.6
【答案】C
【解析】解:∵∠BAC与∠BOC互补,
∴∠BAC+∠BOC=180°,
∵∠BAC= ![]() ∠BOC,
∠BOC,
∴∠BOC=120°,
过O作OD⊥BC,垂足为D,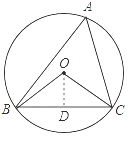
∴BD=CD,
∵OB=OC,
∴OB平分∠BOC,
∴∠DOC= ![]() ∠BOC=60°,
∠BOC=60°,
∴∠OCD=90°﹣60°=30°,
在Rt△DOC中,OC=6,
∴OD=3,
∴DC=3 ![]() ,
,
∴BC=2DC=6 ![]() ,
,
故答案为:C.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。根据定理可得∠BAC= ![]() ∠BOC,再由已知∠BAC与∠BOC互补可求∠BOC的度数,过O作OD⊥BC,垂足为D,根据垂径定理可得BD=CD,OB平分∠BOC,∠OCD的度数可求,在Rt△DOC中,用勾股定理可求DC的长,则线段BC=2DC。
∠BOC,再由已知∠BAC与∠BOC互补可求∠BOC的度数,过O作OD⊥BC,垂足为D,根据垂径定理可得BD=CD,OB平分∠BOC,∠OCD的度数可求,在Rt△DOC中,用勾股定理可求DC的长,则线段BC=2DC。


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.![]() m
m
C.![]() m
m
D.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一可以自由转动的转盘,AB为转盘直径,如图所示,并规定:顾客消费100元(含100元)以上,就能获得一次转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,顾客就可以获得相应的优惠.
(1)某顾客正好消费99元,是否可以获得相应的优惠.
(2)某顾客正好消费120元,他转一次转盘获得三种打折优惠的概率分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
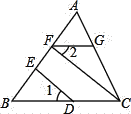
证明:∵CF⊥AB,DE⊥AB (______)
∴∠BED=90°,∠BFC=90° (______)
∴∠BED=∠BFC (______)
∴ED∥FC (______)
∴∠1=∠BCF (______)
∵∠1=∠2 (______)
∴∠2=∠BCF (______)
∴FG∥BC (______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com