
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
【答案】(1)证明见解析;(2)∠EOC的度数为40°;
(3)比值不变,∠OCB:∠OFB=1:2
(4)∠OCA的度数为60°.
【解析】试题分析:(1)根据等式性质及平行线的判定可以得到证明思路;
(2)根据角平分线及观察图形知道∠EOC=![]() ∠BOC=400;
∠BOC=400;
(3)∠OFB与∠OCB实际上是三角形的外角与不相邻的内角的关系,再观察图形可知两直线平行内错角相等,角平分线分得的两个角相等,等量代换可得结论;
(4)由∠OEB=∠OCA可以推出∠BOE=∠BCO=∠EOF=∠COF∠COA=200,从而∠OCA=600;
试题解析:
解:(1)∵BC∥OA,
∴∠B+∠O=180°,又∵∠B=∠A,
∴∠A+∠O=180°,
∴OB∥AC; 3分
(2)∵∠B+∠BOA=180°,∠B=100°,
∴∠BOA=80°,
∵OE平分∠BOF,
∴∠BOE=∠EOF,又∵∠FOC=∠AOC,
∴∠EOF+∠FOC= (∠BOF+∠FOA)= ∠BOA=40°;
(3)结论:∠OCB:∠OFB的值不发生变化.理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
(4)由(1)知:OB∥AC,
则∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
则∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEC=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论: ①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若 ![]() =
= ![]() ,则3S△EDH=13S△DHC , 其中结论正确的有 .
,则3S△EDH=13S△DHC , 其中结论正确的有 . 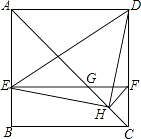
查看答案和解析>>
科目:初中数学 来源: 题型:
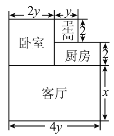
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)当x=4,y=2时,铺1 m2地砖的平均费用为30元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
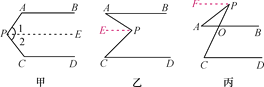
【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过15吨(含15吨)时,每吨按政府补贴优惠价收费;每月超过15吨时,超过部分每吨按市场调节价收费.小明家1月份用水23吨,交水费35元,2月份用水19吨,交水费25元.
(1)求每吨水的政府补贴优惠价与市场调节价分别是多少;
(2)小明家3月份用水24吨,他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一快递小哥骑电动车需要在规定的时间把快递送到某地,若他以![]() 的速度行驶就会提前2分钟到达,如果他以
的速度行驶就会提前2分钟到达,如果他以![]() 的速度行驶就要迟到6分钟。
的速度行驶就要迟到6分钟。
(1)快递小哥行驶的路程是多少千米;
(2)当快递小哥以![]() 的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com