练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为,则这块圆形纸片的直径为( )

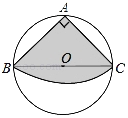
    A. 12cm B. 20cm C. 24cm D. 28cm

    【答案】C

    【解析】分析：设这块圆形纸片的半径为R，圆锥的底面圆的半径为r，利用等腰直径三角形的性质得到AB=R，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到2πr=，解得r=R，然后利用勾股定理得到（R）2=（3）2+（R）2，再解方程求出R即可得到这块圆形纸片的直径．

    详解：设这块圆形纸片的半径为R，圆锥的底面圆的半径为r，则AB=R，根据题意得：

    2πr=，解得：r=R，所以（R）2=（3）2+（R）2，解得：R=12，所以这块圆形纸片的直径为24cm．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2016年共享单车横空出世，较好地解决了人们“最后一公里”出行难的问题．截至2016年年底，“ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍，覆盖城市也远超于“摩拜单车”，“ofo共享单车”注册用户量约为960万人，“摩拜单车”的注册用户量约为750万人，据统计，使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人，假设注册这两种单车的用户都在使用共享单车．

    (1)求2016年“摩拜单车”的投放数量约为多少万台；

    (2)摩拜公司决定2018年在某市采取如下投放方式：甲街区每1000人投放a辆“摩拜单车”，乙街区每1000人投放辆“摩拜单车”．按照这种投放方式，甲街区共投放了1500辆，乙街区共投放了1200辆，如果两个街区共有15万人，试求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出下列4个结论：①4ac－b2＜0；②3b＋2c＜0；③4a＋c＜2b；④m(am＋b)＋b＜a(m≠－1)．其中正确结论的个数是( )

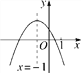
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了给游客提供更好的服务，某景区随机对部分游客进行了关于“景区服务工作满意度”的调查，并根据调查结果绘制成如下不完整的统计图表.

    满意度

    人数

    所占百分比

    非常满意

    12

    10%

    满意

    54

    m

    比较满意

    n

    40%

    不满意

    6

    5%

    根据图表信息，解答下列问题：

    (1)本次调查的总人数为______，表中m的值为_______；

    (2)请补全条形统计图；

    (3)据统计，该景区平均每天接待游客约3600人，若将“非常满意”和“满意”作为游客对景区服务工作的肯定，请你估计该景区服务工作平均每天得到多少名游客的肯定.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

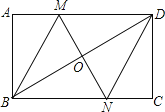
    【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．

    求证：四边形BMDN是菱形；

    若，，求菱形BMDN的面积和对角线MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆，但由于种种原因，实际每天的销售量与计划量相比有出入。下表是某周的销售情况（超额记为正、不足记为负）：

    星期

    一

    二

    三

    四

    五

    六

    日

    与计划量的差值

    +4

    -3

    -5

    +14

    -8

    +21

    -6

    （1）根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。

    （2）根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。

    （3）该店实行每日计件工资制，每销售一辆车可得40元，若超额完成任务，则超过部分每辆另奖15元；少销售一辆扣20元，那么该店铺的销售人员这一周的工资总额是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年学校举行足球联赛，共赛17轮（即每队均需参赛17场），记分办法是：胜1场得3分，平1场得1分，负1场得0分．在这次足球比赛中，小虎足球队得16分，且踢平场数是所负场数的整数倍，则小虎足球队所负场数的情况有（　 ）种

    A. 6 B. 5 C. 4 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学中,为了书写简便，18世纪数学家欧拉就引进了求和符号“∑”.记,，.

    同学们，通过以上材料的阅读，请回答下列问题：

    (1)计算(填写最后的结果)

    =__________；____________.

    (2)2+4+6+8+10用求和公式符号可表示为__________.

    (3)化简：

    (4)若对于任意x都存在，请求代数式b-ab的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有20筐橘子，以每筐20千克为标准，超过或不足的部分分别用正数或负数来表示，记录如下：

    与标准重量的差(单位：千克)

    －2

    －1.5

    －1

    0

    1

    1.5

    筐 数

    1

    4

    2

    3

    2

    8

    (1)求最重的一筐比最轻的一筐重多少？

    (2)求20筐橘子的总重量是多少千克？

    查看答案和解析>>

    同步练习册答案