
����Ŀ��2016�깲��������ճ������Ϻõؽ�������ǡ����һ��������ѵ����⣮����2016����ף���ofo������������Ͷ�������ǡ�Ħ�ݵ�����Ͷ��������1.6�������dz���ҲԶ���ڡ�Ħ�ݵ���������ofo����������ע���û���ԼΪ960���ˣ���Ħ�ݵ�������ע���û���ԼΪ750���ˣ���ͳ�ƣ�ʹ��һ����ofo������������ƽ��������ʹ��һ����Ħ�ݵ�������ƽ��������3�ˣ�����ע�������ֵ������û�����ʹ�ù���������
(1)��2016�ꡰĦ�ݵ�������Ͷ������ԼΪ������̨��
(2)Ħ�ݹ�˾����2018����ij�в�ȡ����Ͷ�ŷ�ʽ������ÿ1000��Ͷ��a����Ħ�ݵ��������ҽ���ÿ1000��Ͷ��![]() ����Ħ�ݵ���������������Ͷ�ŷ�ʽ��������Ͷ����1500�����ҽ�����Ͷ����1200�������������������15���ˣ�����a��ֵ��
����Ħ�ݵ���������������Ͷ�ŷ�ʽ��������Ͷ����1500�����ҽ�����Ͷ����1200�������������������15���ˣ�����a��ֵ��
���𰸡���1��2016�ꡰĦ�ݵ�������Ͷ������ԼΪ50��̨����2��a��ֵΪ15.
��������
��1����2016����Ħ�ݵ�������Ͷ������ԼΪx��̨�����������г���ʽ���̽�ɣ�
��2�� ����������������15�����г�����a�ķ��̽��.
�⣺(1)��2016����Ħ�ݵ�������Ͷ������ԼΪx��̨��
�������⣬��![]() .
.
���x��50.
�����飬x��50��ԭ���̵Ľ⣬�ҷ������⣮
��2016����Ħ�ݵ�������Ͷ������ԼΪ50��̨��
(2)����ɵ�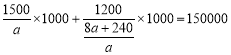 ��
��
���a��15.
�����飬a��15�����з��̵Ľ⣬�ҷ������⣮
��a��ֵΪ15.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��BC���ӳ����ϣ���CE=BC��AE=AB��AE��DC�ཻ�ڵ�O������DE��
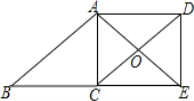
��1����֤���ı���ACED�Ǿ��Σ�
��2������AOD=120����AC=4����Խ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x���ཻ��A����3��0����B��1��0�����㣬��y���ཻ�ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��

��1����D�����ꣻ
��2������κ����Ľ���ʽ��
��3������ͼ��ֱ��д��ʹһ�κ���ֵС�ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±���

���ǰ�ijһ����������ĸ��ӵõ��Ķ���ʽ��Ϊ��������ʽ�����磺��1��ġ���������ʽ��Ϊx��4y.
�ش��������⣺
�� ��4��ġ���������ʽ��Ϊ������������n��ġ���������ʽ��Ϊ����������
�� ����1��ġ���������ʽ����ֵΪ2����2��ġ���������ʽ����ֵΪ��6.
�� ��x��y��ֵ��
�� �ڢٵ������£���n��ġ���������ʽ��ֵ������n�ı仯���仯������������ʽ��ֵ�������ֵ����ʱnֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ�����ͼ����㣨0,3�����������������ڵ�һ������Χ�ɵ����������Ϊ3�������һ�κ����ı���ʽΪ�� ��
A.y=1.5x+3B.y=1.5x-3C.y=-1.5x+3D.y=-1.5x-3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��F�ֱ��DZ�AD��BC�ϵĵ㣬��AE=CF��ֱ��EF�ֱ�BA���ӳ��ߡ�DC���ӳ����ڵ�G��H����BD�ڵ�O��
��1����֤����ABE�ա�CDF��
��2������DG����DG=BG�����ı���BEDF��ʲô�����ı��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
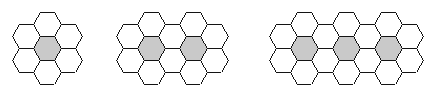
����Ŀ���úڰ�������ɫ���������ε�ש��������ʾ�Ĺ���ƴ������ͼ����
![]() ��������
�������� ![]() ��
��![]()
�� ����שn��1ʱ����ש��_______�飬����שn��2ʱ����ש��________�飬
����שn��3ʱ����ש��_______�飮
�� ��n��ͼ���У���ɫ��ש�� �飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,����ABCD�Ķ���C��ԭ��O�غ�,��B��y�����������,��A�ڷ���������![]() (x>0)��ͼ����,��D������Ϊ(4,3).��AB���ڵ�ֱ�߽���ʽΪ
(x>0)��ͼ����,��D������Ϊ(4,3).��AB���ڵ�ֱ�߽���ʽΪ![]() ����������ABCD��x��������ƽ��m����λ��
����������ABCD��x��������ƽ��m����λ��
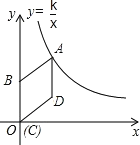
�ٵ����εĶ���B���ڷ�����������ͼ���ϣ���m��ֵ��
����ƽ���У�������������ͼ�������εı�ADʼ���н��㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ��Բ��ֽƬ�ϼ���һ��Բ�Ľ�Ϊ90�������ABC,ʹ��A��B��C��Բ����,�����µ�������Ϊһ��Բ����,���Բ�ĸ�Ϊ![]() ,�����Բ��ֽƬ��ֱ��Ϊ( )
,�����Բ��ֽƬ��ֱ��Ϊ( )
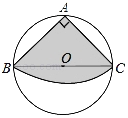
A. 12cm B. 20cm C. 24cm D. 28cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com