
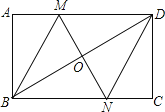
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:
(1)先由已知条件证四边形BMDN是平行四边形,结合MN垂直平分BD即可得到平行四边形BMDN是菱形;
(2)设BM=x,由四边形BMDN是菱形可得DM=BM=x,由此可得AM=AD-DM=8-x,这样在Rt△ABM中由勾股定理可求得x=5,这样由S菱形BMDN=MD·AB即可求出其面积了;在Rt△ABD中由已知易得BD=![]() ,结合S菱形BMDN=MD·AB=
,结合S菱形BMDN=MD·AB=![]() BD·MN即可求得MN的长.
BD·MN即可求得MN的长.
(1)∵四边形ABCD是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
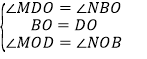 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形BMDN是平行四边形,
∵![]() ,
,
∴平行四边形BMDN是菱形.
(2)∵四边形BMDN是菱形,
∴![]() ,
,
设MD长为x,则![]() ,
,
在![]() 中,
中,![]()
即![]() ,
,
解得:![]() ,
,
即![]() .
.
菱形BMDN的面积![]() ,
,
∵![]() ,
,
又∵菱形BMDN的面积![]() ,
,
∴![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3B.y=1.5x-3C.y=-1.5x+3D.y=-1.5x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
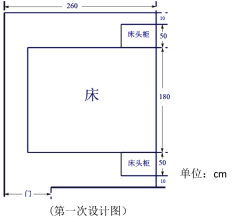
【题目】小丽家在装修,虽然房间比较小,但是小丽总想睡1.8米宽的大床,那样抱着她的大娃娃睡多好啊,妈妈说:“你已经八年级了,自己设计一下,怎样可以把1.8米宽的床放好,并且还比较美观?”下面是小丽的第一次设计图:1.8米宽的床一般长2.2米,床头柜一般需要50cm,门宽80cm,只能往房里开。
妈妈看了设计图以后,怀疑地说:“像你这样设计,门好像打不开啊。”请通过计算说明,此时门能否完全打开?
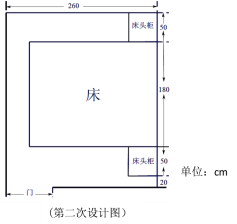
小丽考虑将家具整体平移一下,她又设计了第二种方案,这时妈妈看了一会,问小丽:“你确定门能完全打开?”,小丽得意地笑了,请通过计算说明为什么这次可以了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(﹣1,n)和Q(3,n)都在二次函数y=x2+bx﹣1的图象上.
(1)求b、n的值;
(2)将二次函数图象向上平移几个单位后,得到的图象与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为![]() ,则这块圆形纸片的直径为( )
,则这块圆形纸片的直径为( )
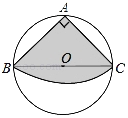
A. 12cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
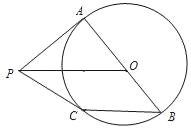
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 C、D是线段AB上两点(不与端点A、B重合),点A、B、C、D四点组成的所有线段的长度都是正整数,且总和为29,则线段AB的长度为__________________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com