
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
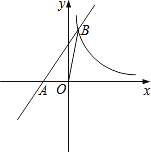
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 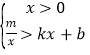 的解集.
的解集.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
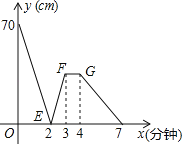
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 m,甲机器人前2min的速度为 m/min.
(2)若前3min甲机器人的速度不变,求出前3min,甲、乙两机器人之间的距离y(m)与他们的行走时间r(min)之间的关系式.
(3)求出两机器人出发多长时间相距28m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在复习课上,wsy老师要求写出几个与实数有关的结论:小明同学写了以下5个:
①任何无理数都是无限不循环小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有![]() 这5个;
这5个;
④![]() 是分数,它是有理数;
是分数,它是有理数;
⑤由四舍五入得到的近似数7.30表示大于或等于7.295,而小于7.305的数.其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.
(1)求A、B、C三点的坐标,并求出△ABC的面积;
(2)将抛物线向左或向右平移,得到抛物线L,且L与x轴相交于A、B两点(点A在点B的左侧),并与y轴交于点C,要使△ABC和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD⊥CD,BC⊥CD,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F。
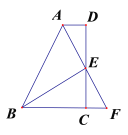
证明:(1)FC=AD;
(2)AB=BC+AD。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解本校七年级学生课后延时服务课外阅读情况,随机抽取该校七年级部分学生进行问卷调查(每人只选一种书籍),如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
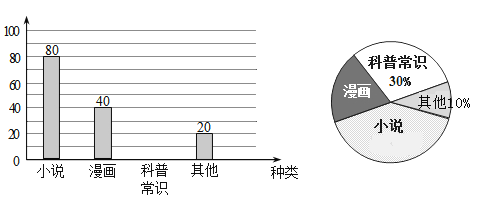
(1)这次活动一共调查了________名学生;
(2)在扇形统计图中,“小说”所在扇形的圆心角等于________;
(3)补全条形统计图.
(4)若该校七年级学生720人,试求出该年级阅读漫画的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在平面直角坐标系中,抛物线y=x![]() +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x![]() +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为![]() ,与x轴交于
,与x轴交于![]() 、
、![]() 两点,与y轴交于
两点,与y轴交于![]() 点,在以A、B、C、M、
点,在以A、B、C、M、![]() 、
、![]() 、
、![]() 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com