
【题目】已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.
(1)求A、B、C三点的坐标,并求出△ABC的面积;
(2)将抛物线向左或向右平移,得到抛物线L,且L与x轴相交于A、B两点(点A在点B的左侧),并与y轴交于点C,要使△ABC和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.
【答案】(1)A(-3,0),B(2,0),C(0,6);15;(2)y=x2-7x-6,y=x2+7x-6,y=x2-x-6.
【解析】(1)在抛物线解析式中分别令x=0、y=0即可求得抛物线与坐标轴的交点坐标,然后根据三角形面积公式即可求得三角形的面积;
(2)将抛物线向左或向右平移时,A、B两点间的距离不变,始终为5,那么要使△ABC和△ABC的面积相等,高也只能是6,分点C在x轴上方与x轴下方两种情况分别讨论即可得.
(1)当y=0时,x2+x-6=0,解得x1=-3,x2=2,
当x=0时,y=-6,
∴A(-3,0),B(2,0),C(0,6),
∴S△ABC=![]() AB·OC=
AB·OC=![]() ×5×6=15;
×5×6=15;
(2)将抛物线向左或向右平移时,A、B两点间的距离不变,始终为5,
那么要使△ABC和△ABC的面积相等,高也只能是6,
设A(a,0),则B(a+5,0),y=(x-a)(x-a-5),
当x=0时,y=a2+5a,
当C点在x轴上方时,y=a2+5a=6,a=1或a=-6,
此时y=x2-7x-6或y=x2+7x-6;
当C点在x轴下方时,y=a2+5a=-6,a=-2或a=-3,
此时y=x2-x-6或y=x2+x-6(与原抛物线重合,舍去);
所以,所有满足条件的抛物线的函数表达式为:y=x2-7x-6,y=x2+7x-6,y=x2-x-6.


科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求![]() 的值.
的值.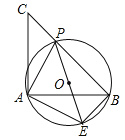
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游公司大巴从旅行社出发,先向西行驶3千米到达![]() 景点,再继续向西行驶2千米到达
景点,再继续向西行驶2千米到达![]() 景点,然后向东行驶7千米到达
景点,然后向东行驶7千米到达![]() 景点,最后回到旅行社.
景点,最后回到旅行社.
(1)以旅行社为原点,以向东方向为正方向,用1个单位长度表示1千米,画出数轴,并在该数轴上表示出![]() 、
、![]() 、
、![]() 三个景点的位置.
三个景点的位置.
(2)![]() 景点距离
景点距离![]() 景点多远?
景点多远?
(3)该旅游大巴共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
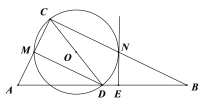
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
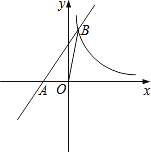
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 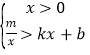 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,解答后面的问题:“十字相乘法”能将二次三项式分解因式,对于形如![]() 的关于
的关于![]() ,
,![]() 的二次三项式来说,方法的关键是将
的二次三项式来说,方法的关键是将![]() 项系数
项系数![]() 分解成两个因数
分解成两个因数![]() ,
,![]() 的积,即
的积,即![]() ,将
,将![]() 项系数
项系数![]() 分解成两个因式
分解成两个因式![]() ,
,![]() 的积,即
的积,即![]() ,并使
,并使![]() 正好等于
正好等于![]() 项的系数
项的系数![]() ,那么可以直接写成结果:
,那么可以直接写成结果:![]()
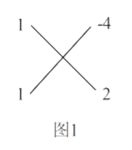
例:分解因式:![]()
解:如图1,其中![]() ,
,![]() ,而
,而![]()
所以![]()
而对于形如![]() 的关于
的关于![]() ,
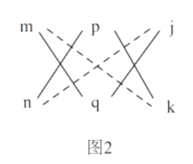
,![]() 的二元二次式也可以用十字相乘法来分解.如图2.将
的二元二次式也可以用十字相乘法来分解.如图2.将![]() 分解成
分解成![]() 乘积作为一列,
乘积作为一列,![]() 分解成
分解成![]() 乘积作为第二列,
乘积作为第二列,![]() 分解成
分解成![]() 乘积作为第三列,如果
乘积作为第三列,如果![]() ,
,![]() ,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式
,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式![]()
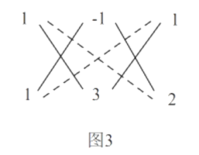
例:分解因式![]()
解:如图3,其中![]() ,
,![]() ,
,![]()
而![]() ,
,![]() ,
,![]()
所以![]()
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:①![]() .
.
②![]() .
.
(2)若关于![]() ,
,![]() 的二元二次式
的二元二次式![]() 可以分解成两个一次因式的积,求
可以分解成两个一次因式的积,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
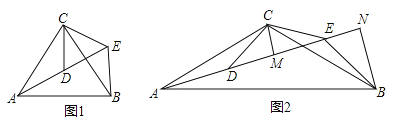
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com