
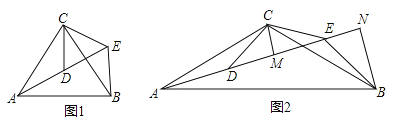
【题目】(2016山东省菏泽市)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
【答案】(1)①证明见解析;②80°;(2)证明见解析.
【解析】试题(1)①通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数;
(2)根据等腰三角形的性质结合顶角的度数,即可得出底角的度数,利用(1)的结论,通过解直角三角形即可求出线段AD、DE的长度,二者相加即可证出结论.
试题解析:(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°.
∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE.
∵△ACB和△DCE均为等腰三角形,∴AC=BC,DC=EC.
在△ACD和△BCE中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ACD≌△BCE(SAS),∴AD=BE.
②解:∵△ACD≌△BCE,∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°.
∵∠BEC=∠CED+∠AEB,且∠CED=50°,∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.
(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=![]() ×(180°﹣120°)=30°.
×(180°﹣120°)=30°.
∵CM⊥DE,∴∠CMD=90°,DM=EM.
在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×![]() =
=![]() CM.
CM.
∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.
在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE=![]() =
=![]() BN.
BN.
∵AD=BE,AE=AD+DE,∴AE=BE+DE=![]() CM+
CM+![]() BN.
BN.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),已知直线AC与双曲线y=![]() (m≠0)在第一象限内有一交点Q(5,n).
(m≠0)在第一象限内有一交点Q(5,n).
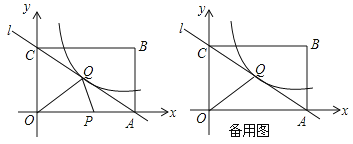
(1)求直线AC和双曲线的解析式;
(2)若动点P从A点出发,沿折线AO→OC的路径以每秒2个单位长度的速度运动,到达C处停止.求△OPQ的面积S与的运动时间t秒的函数关系式,并求当t取何值时S=10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖,
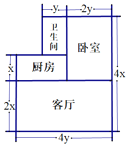
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以下各图都是由同样大小的图形①按一定规律组成,其中第①个图形中共有1个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑦个图形中完整菱形的个数为( )

A. 83B. 84C. 85D. 86
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC于点D.
(1)求证:△BCD为等腰三角形;
(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;
(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-![]() )2 016化为(
)2 016化为(![]() )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
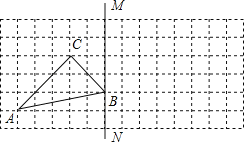
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com