
【题目】甲、乙两名工人分别加工a个同种零件.甲先加工一段时间,由于机器故障进行维修后继续按原来的工作效率进行加工,当甲加工![]() 小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
(1)甲的工作效率为 个/时,维修机器用了 小时
(2)乙的工作效率是 个/时;问题解决:
①乙加工多长时间与甲加工的零件数量相同,并求此时乙加工零件的个数;
②若乙比甲早10分钟完成任务,求a的值.
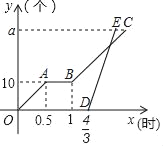
【答案】(1)20,0.5;(2)60;(3)①乙加工![]() 小时与甲加工零件数量相同,此时乙加工25个零件;②a=30
小时与甲加工零件数量相同,此时乙加工25个零件;②a=30
【解析】
(1)、根据图象可以的到甲0.5小时加工了10个零件,则可以求得甲的效率,根据图象可以直接求出甲维修机器所用时间;(2)、根据乙的效率是甲的3倍即可求得乙的效率;①、利用待定系数法求得乙的函数解析式以及甲在大于1小时时的函数解析式,求两个函数的交点;②、设乙加工零件m 个,则点E(x1,a),点C(x2,a),分别代入两个函数的解析式,根据x2-x1=![]() 小时,即可列方程组求解.
小时,即可列方程组求解.
(1)甲的工作效率是10÷0.5=20(个/时),维修机器用的时间为:1﹣0.5=0.5(小时).
(2)∵乙的工作效率是甲的工作效率的3倍,甲的工作效率是20个/时,
∴乙的工作效率是20×3=60(个/时).
(3)①设直线BC对应的函数关系式为y=20x+b1,把点B(1,10)代入得b1=﹣10.
则直线BC所对应函数关系式为y=20x﹣10 ①.设直线DE的关系式为y=60x+b2,
把点D(![]() ,0)代入得b2=﹣80.则直线DE对应的函数关系式为y=60x﹣80②.﹣
,0)代入得b2=﹣80.则直线DE对应的函数关系式为y=60x﹣80②.﹣
联立①②,得:![]() ,解得:
,解得:![]() ,所以交点坐标为(1.75,25).
,所以交点坐标为(1.75,25).
1.75﹣1.75﹣![]() =
=![]() (小时).
(小时).
所以乙加工![]() 小时与甲加工零件数量相同,此时乙加工25个零件;
小时与甲加工零件数量相同,此时乙加工25个零件;
②设点E(x1,a),点C(x2,a),分别代入y=60x﹣80,y=20x﹣10,
得x1=![]() ,x2=
,x2=![]() ,∵x2﹣x1=
,∵x2﹣x1=![]() =
=![]() ,∴
,∴![]() ﹣
﹣![]() =
=![]() ,解得:a=30.
,解得:a=30.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线 y=2x2﹣4x+m 的图象的部分如图所示,则关于 x 的一元二次方程 2x2﹣4x+m=0 的解是 x1=______,x2=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB,ED,延长BE交AD于点F.若∠DEB=140°,则∠AFE的度数为( )
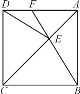
A. 65° B. 70° C. 60° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险?请用你学过的知识加以解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点![]() 、点
、点![]() 在网格中的位置如图所示.
在网格中的位置如图所示.
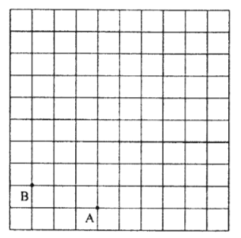
(1)建立适当的平面直角坐标系,使点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ;
;
(2)点![]() 的坐标为
的坐标为![]() ,在平面直角坐标系中标出点
,在平面直角坐标系中标出点![]() 的位置,连接
的位置,连接![]() 、
、![]() 、
、![]() ,
,
(3)若![]() 各项点的横坐标不变,纵坐标均乘以
各项点的横坐标不变,纵坐标均乘以![]() 在图中做出对应图形
在图中做出对应图形![]() ;
;
(4)![]() 与
与![]() 的位置关系为______;
的位置关系为______;![]() 的面积为______.
的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题不正确的是( )
A.月球距离地球表面约384000000米,用科学记数法表示为3.84×108米
B.用四舍五入法对0.05049取近似值为0.050(精确到0.001)
C.若代数式![]() 有意义,则x的取值范围是x≠2且x≠﹣2
有意义,则x的取值范围是x≠2且x≠﹣2
D.数据1、2、3、4的中位数是2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
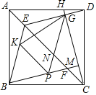
【题目】如图,四边形![]() 为正方形,
为正方形,![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在线段
,在线段![]() 上作
上作![]() ,连接
,连接![]() ,
,![]() ,其中
,其中![]() 交
交![]() 于
于![]() 点,
点,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com