
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
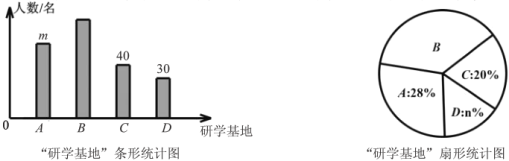
(1)统计图中![]() ______,
______,![]() ______;
______;
(2)若该校有1500名学生,请估计选择![]() 基地的学生人数;
基地的学生人数;
(3)某班在选择![]() 基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
【答案】(1)56,15;(2)555;(3)![]()
【解析】
(1)根据C基地的调查人数和所在的百分比即可求出调查总人数,再乘调查A基地人数所占的百分比即可求出m,用调查D基地的人数除以调查总人数即可求出n;
(2)先求出调查B基地人数所占的百分比,再乘1500即可;
(3)根据题意,列出表格,然后利用概率公式求概率即可.
(1)调查总人数为:40÷20%=200(人)
则m=200×28%=56(人)
n%=30÷200×100%=15%
∴n=15.
故答案为:56;15
(2)![]() (人)
(人)
答:选择![]() 基地的学生人数为555人.
基地的学生人数为555人.
(3)根据题意列表如下:
男1 | 男2 | 男3 | 男4 | 女1 | 女2 | |
男1 | (男1,男2) | (男1,男3) | (男1,男4) | (男1,女1) | (男1,女2) | |
男2 | (男2,男1) | (男2,男3) | (男2,男4) | (男2,女1) | (男2,女2) | |
男3 | (男3,男1) | (男3,男2) | (男3,男span>4) | (男3,女1) | (男3,女2) | |
男4 | (男4,男1) | (男4,男2) | (男4,男3) | (男4,女1) | (男4,女2) | |
女1 | (女1,男1) | (女1,男2) | (女1,男3) | (女1,男4) | (女1,女2) | |
女2 | (女2,男1) | (女2,男2) | (女2,男3) | (女2,男4) | (女2,女1) |
由上表可知,共有30种等可能的结果,其中“1男1女”的结果有16种.
所以:![]() (1男1女)
(1男1女)![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】为了促进旅游业的发展,某市新建一座景观桥.桥的拱肋ADB可视为抛物线的一部分,桥面AB可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度AB为40米,桥拱的最大高度CD为16米(不考虑灯杆和拱肋的粗细),求与CD的距离为5米的景观灯杆MN的高度.
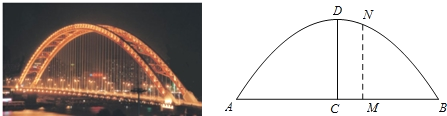
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
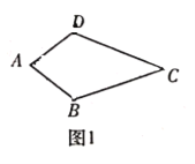
③神奇四边形的中点四边形是
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
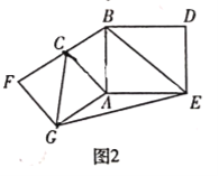
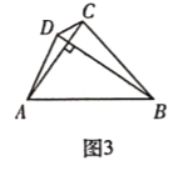
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的8×10方格纸,方格纸中的每个小正方形的边长均为1,点A,B,C均位于格点处,请按要求画出格点四边形(四边形各顶点都在格点上).
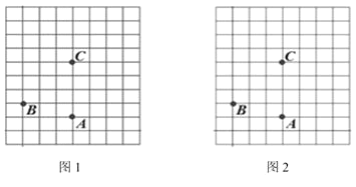
(1)在图1中画出一个以点A,B,C,P为顶点的格点四边形,且为中心对称图形.
(2)在图2中画出一个以点A,B,C,Q为顶点的格点四边形,AC平分∠BCQ,且有两个内角为90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
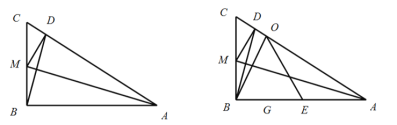
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A.顺次联结任意四边形四边中点所得的四边形是平行四边形
B.顺次联结对角线相等的四边形四边中点所得的四边形是菱形
C.顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形
D.顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
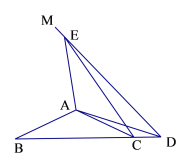
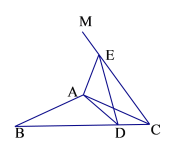
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
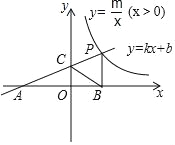
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)根据图象直接写出kx+b<![]() 的x的取值范围;
的x的取值范围;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com