
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
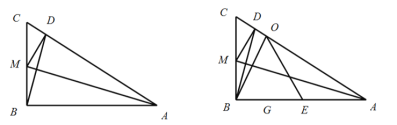
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
【答案】(1) ![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或20.
或20.
【解析】
(1)设BD与AM交于点N,那么∠BNM=90°,BN=DN,然后解直角三角形即可解答;
(2)先确定∠CAB的正弦值,再设BG=3m、OG=4m建立方程求得m;再运用解直角三角形求得BE,最后利用AE=AB-BE即可求解;
(3)先求出△AOE为等腰三角形时圆O的半径及圆心距;然后就圆A与圆O是内切还是外切分类讨论求解即可.
解:(1)如图:设BD与AM交于点N,那么∠BNM=90°,BN=DN
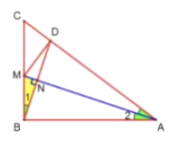
∵Rt△ABM中,AB=12,BM=4,
∴tan∠2=![]() , cos∠2=
, cos∠2=![]()
∵∠1+∠BMN=90°,∠2+∠BMN=90°,
∴∠1=∠2.
∵Rt△BMN中,BM=4,
∴BN=BM·cos∠1=![]()
∴BD=2BN=![]()
如图所示:作DH⊥AB于H,
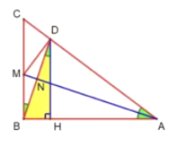
∴DH∥CB
∴∠BDH=∠MBN
∴DH=BD·cos∠BDH=![]() ×
×![]() =
=![]() ;
;
(2)∵在Rt△ADH中,DH=![]() ,AD=AB=12,
,AD=AB=12,
∴sin∠CAB=![]()
如图所示:因为点F平分弧BE,
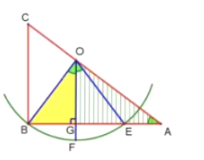
∴OF⊥BE,BG=EG
在Rt△BOG中,已知∠BOF=∠BAC,设BG=3m,OG=4m.
在Rt△AOG中,由tan∠A=![]() =
=![]() ,
,
解得m=![]()
∴AE=AB-BE=12-6m=![]() ;
;
(3)第一步,求△AOE为等腰三角形时圆O的半径,
∵△AOE是钝角三角形,
∴只存在EO=EA的情况。
如图所示:作EK⊥AC于K
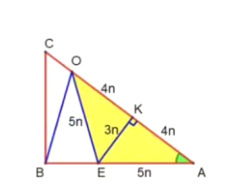
在Rt△AEK中,设EK=3n,则AK=4n,EA=5n.
如图所示:作OP⊥AB于P
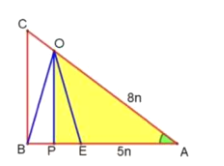
在Rt△AOP中,OA=2AK=8n,AP=![]() OA=
OA=![]()
∴PE=AP-AE=![]() -5n=
-5n=![]()
由AB=2PE+EA=![]() +5n=12.解得:n=
+5n=12.解得:n=![]() .
.
∴ro=OE=5n=![]() ,圆心距d=OA=
,圆心距d=OA=![]()
第二步,分两种情况讨论圆A与圆O相切.
①如图所示,当圆A与圆O外切时,ro+ra=d,
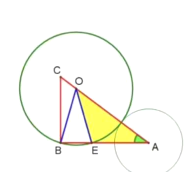
所以ra =d-ro=![]() ;
;
②如图所示,当圆A与圆O内切时ra-ro=d
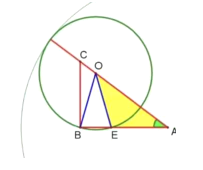
所以ra=d+ro=![]() .
.


科目:初中数学 来源: 题型:
【题目】小雨利用几何画板探究函数y=![]() 图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
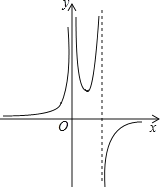
A.a>0,b>0,c=0B.a<0,b>0,c=0
C.a>0,b=0,c=0D.a<0,b=0,c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌
的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成53°角时,测得信号塔
.当太阳光线与水平线成53°角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(tan53°≈1.3)( ).
的高约为(tan53°≈1.3)( ).
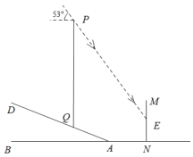
A.10.4B.11.9C.11.4D.13.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)过A(-1,1),B(3,1),C(-2,y1),D(2,y2)四点,则y1与y2的大小关系是( )
A.y1>y2B.y1=y2C.y1<y2D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax-4ax交x轴于点A,直线y= ![]() x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
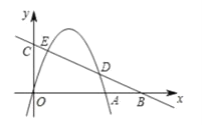
(1)求点A,B,C的坐标.
(2)当点D为BC的中点时,求a的值.
(3)若设抛物线的顶点为点M,点M关于直线BC的对称点为N, 当点N落在△BOC的内部时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
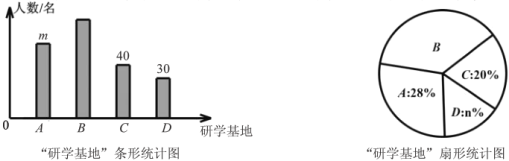
(1)统计图中![]() ______,
______,![]() ______;
______;
(2)若该校有1500名学生,请估计选择![]() 基地的学生人数;
基地的学生人数;
(3)某班在选择![]() 基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从甲地出发以每小时80 km的速度匀速驶往乙地,一段时间后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.货车行驶2.5 h后,在距乙地160 km处与轿车相遇.图中线段AB表示货车离乙地的距离y1 km与货车行驶时间x h的函数关系.
(1)求y1与x之间的函数表达式;
(2)若两车同时到达各自目的地,在同一坐标系中画出轿车离乙地的距离y2与x的图像,求该图像与x轴交点坐标并解释其实际意义.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
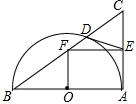
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com