
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
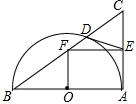
A.7B.8C.9D.10
【答案】C
【解析】
连结AD,先证明E是AC的中点,可知EF、OF是△ABC的中位线,于是可求出AC及BC的长,再证明△CDA∽△CAB,根据相似的性质即可求出CD的长.
解:连结AD,如图,
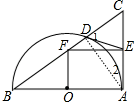
∵∠BAC=90°,AB为直径,
∴AC是⊙O的切线,
∵DE为⊙O的切线,
∴ED=EA,
∴∠ADE=∠2,
∵AB为直径,
∴∠ADB=90°,
∴∠1+∠ADE=90°,∠2+∠C=90°,
∴∠1=∠C,
∴ED=EC,
∴CE=AE,
∵EF∥AB,
∴EF为△ABC的中位线,
∴BF=CF,
而BO=AO,
∴OF为△ABC的中位线,
∴OF∥AE,
∴AE=OF=7.5,
∴AC=2AE=15,
在Rt△ACD中,BC=![]() =
=![]() =25,
=25,
∵∠DCA=∠ACB,
∴△CDA∽△CAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=9.
故选:C.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
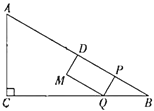
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
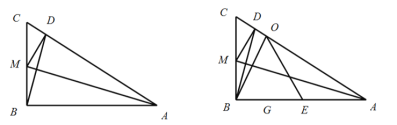
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A.顺次联结任意四边形四边中点所得的四边形是平行四边形
B.顺次联结对角线相等的四边形四边中点所得的四边形是菱形
C.顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形
D.顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?
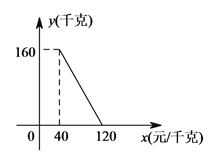
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
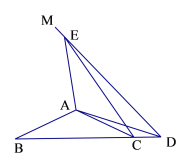
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
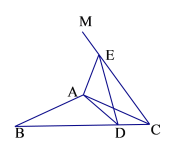
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位向终点
个单位向终点![]() 匀速运动(点
匀速运动(点![]() 不与
不与![]() 、
、![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() .以
.以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形不是矩形时,求
重叠部分图形不是矩形时,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)沿直线![]() 将矩形
将矩形![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
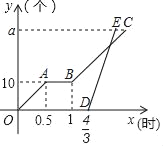
【题目】甲、乙两名工人分别加工a个同种零件.甲先加工一段时间,由于机器故障进行维修后继续按原来的工作效率进行加工,当甲加工![]() 小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
(1)甲的工作效率为 个/时,维修机器用了 小时
(2)乙的工作效率是 个/时;问题解决:
①乙加工多长时间与甲加工的零件数量相同,并求此时乙加工零件的个数;
②若乙比甲早10分钟完成任务,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
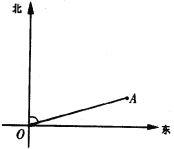
【题目】如图,灯塔A周围1000米水域内有礁石,一舰艇由西向东航行,在O处测得灯塔A在北偏东74°方向线上,这时O、A相距4200米,如果不改变航向,此舰艇是否有触礁的危险?(指定数学课使用科学计算器的地区的考生须使用计算器计算.以下数据供计算器未进入考场的地区的考生选用:cos74°=0.2756,sin74°=0.9613,cot74°=0.2867,tan74°=3.487)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com