
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?
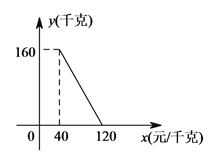
【答案】(1)y=-2x+240(40≤x≤120)(2) 销售单价应定为100元
【解析】
(1)设出函数解析式y=kx+b,把点(40,160),(120,0)代入,即可求出函数解析式.
(2)根据成本不超过3000元,进价×销售量≤3000,列不等式40(-2x+240)≤3000,解不等式求出x≥82.5,结合图形得出xd的取值范围82.5≤x≤120.再根据每千克的利润×销售量列出一元二次方程(x-40)(-2x+240)=2400,解方程得出![]() ,根据x的取值范围,得出销售价应为100元.
,根据x的取值范围,得出销售价应为100元.
(1)设y与x函数关系式y=kx+b,把点(40,160),(120,0)代入得
![]() 解得
解得![]()
∴y与x函数关系式为y=-2x+240(40≤x≤120).
(2)由题意,销售成本不超过3000元,得
40(-2x+240)≤3000.
解不等式得x≥82.5,
∴82.5≤x≤120.
根据题意列方程,得(x-40)(-2x+240)=2400.
即x2-160x+6000=0,
解得x1=60,x2=100.
∵60<82.5,故舍去.
∴销售单价应该定为100元.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
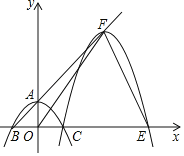
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax-4ax交x轴于点A,直线y= ![]() x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
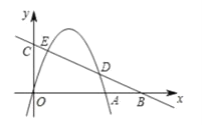
(1)求点A,B,C的坐标.
(2)当点D为BC的中点时,求a的值.
(3)若设抛物线的顶点为点M,点M关于直线BC的对称点为N, 当点N落在△BOC的内部时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从甲地出发以每小时80 km的速度匀速驶往乙地,一段时间后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.货车行驶2.5 h后,在距乙地160 km处与轿车相遇.图中线段AB表示货车离乙地的距离y1 km与货车行驶时间x h的函数关系.
(1)求y1与x之间的函数表达式;
(2)若两车同时到达各自目的地,在同一坐标系中画出轿车离乙地的距离y2与x的图像,求该图像与x轴交点坐标并解释其实际意义.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.

(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
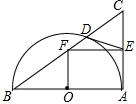
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 和抛物线
和抛物线![]() 相交于点
相交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线
是抛物线![]() 上
上![]() 段的一点(点
段的一点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线
轴的垂线交抛物线![]() 于点
于点![]() ,以
,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,当正方形的四个顶点分别落在四个不同象限时,
,当正方形的四个顶点分别落在四个不同象限时,![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
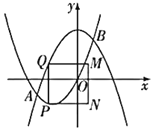
【题目】问题提出
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
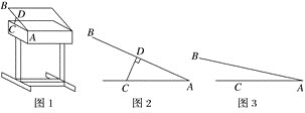
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com