
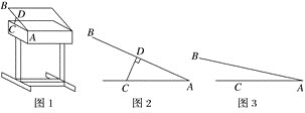
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
【答案】解:(1)在Rt△ADC中,AC=30,∠DAC=24°,sin∠DAC=![]() ,
,
∴DC=AC·sin∠DAC ≈30×0.40=12.…………………………3分
答:支撑臂DC的长为12 cm.
(2)本题分两种情况,
过点C作CE⊥AB,垂足为E.
在Rt△ACE中,AC=30,∠EAC=12°,sin∠EAC=![]() ,
,
∴CE=AC·sin∠EAC ≈30×0.20=6.…………………………4分
【解析】
(1)∵在Rt△ADC中,AC=30,∠DAC=24°,Sin∠DAC=![]()
∴DC=AC·Sin∠DAC=30×0.40=12
答:支撑臂CD的长为12. …………………………………2分
(2)本题分两种情况。
过C作CE⊥AB,垂足为E.
在Rt△ACE中,AC="30," ∠EAC=12°,Sin∠EAC=![]()
∴CE=AC·Sin∠EAC=30×0.20=6
∴AE=![]()
∵在Rt△EDC中,DC=12,CE=6,
∴DE=![]() ………………………4分
………………………4分
∴AD=12±![]() …………………………………………………………6分
…………………………………………………………6分


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
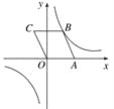
【题目】如图,在平面直角坐标系中,ABCO的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=![]() (k≠0)的图象经过点B.
(k≠0)的图象经过点B.
(1)直接写出点B坐标.
(2)求反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是BC,AB, AC的中点,则下列四个判断中不一定正确的是( )
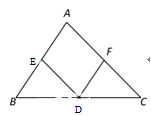
A. 四边形AEDF一定是平行四边形
B. 若∠A=90°,则四边形AEDF是矩形
C. 若AD平分∠A,则四边形AEDF是正方形
D. 若AD⊥BC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
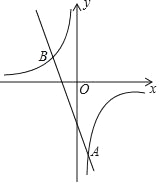
【题目】如图,在平面直角坐标系中,一次函数y=﹣2x+b的图象与反比例函数y=![]() 的图象交于点A(1,n)、B(﹣2,2).
的图象交于点A(1,n)、B(﹣2,2).
(1)求k、n、b的值;
(2)若x轴正半轴上有一点M,满足△MAB的面积为12,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形养鸡场的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
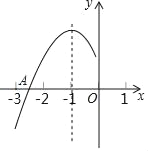
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
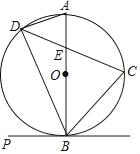
【题目】如图,C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CEDE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com