Question

【题目】如图，在△ABC中，点D，E，F分别是BC，AB， AC的中点，则下列四个判断中不一定正确的是（ ）

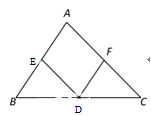
A. 四边形AEDF一定是平行四边形

B. 若∠A=90°，则四边形AEDF是矩形

C. 若AD平分∠A，则四边形AEDF是正方形

D. 若AD⊥BC，则四边形AEDF是菱形

Answer 1

【答案】C

【解析】

一组对边平行且相等的四边形是平行四边形；有一个角是直角的平行四边形是矩形；对角线互相垂直的平行四边形是菱形．

A、∵点D、E、F分别是△ABC三边的中点，∴DE、DF为△ABC得中位线，

∴ED∥AC，且ED=AC=AF；同理DF∥AB，且DF=AB=AE，

∴四边形AEDF一定是平行四边形，正确．

B、若∠A=90°，则四边形AEDF是矩形，正确；

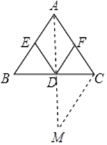
C、若AD平分∠A，如图，延长AD到M，使DM=AD，连接CM，由于BD=CD，DM=AD，

∠ADB=∠CDM，（SAS）∴△ABD≌△MCD∴CM=AB，又∵∠DAB=∠CAD，

∠DAB=∠CMD，∴∠CMD=∠CAD，∴CA=CM=AB，因AD平分∠A

∴AD⊥BC，则△ABD≌△ACD；AB=AC，AE=AF，

结合（1）四边形AEDF是菱形，因为∠A不一定是直角

∴不能判定四边形AEDF是正方形；

D、若AD⊥BC，则△ABD≌△ACD；AB=AC，AE=AF，结合（1）四边形AEDF是菱形，正确．

故选C．