
【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由全等三角形的判定定理SAS证得△ABE≌△DCF;
(2)利用(1)中的全等三角形的对应角相等证得∠AEB=∠DFC,则∠AEF=∠DFE,所以根据平行线的判定可以证得AE∥DF.由全等三角形的对应边相等证得AE=DF,则易证得结论.
解:(1)如图,∵AB∥CD,∴∠B=∠C.
∵在△ABE与△DCF中,AB=CD,∠B=∠C,BE=CF,
∴△ABE≌△DCF(SAS).
(2)如图,连接AF、DE,
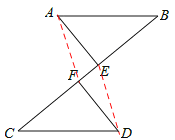
由(1)知,△ABE≌△DCF,
∴AE=DF,∠AEB=∠DFC.
∴∠AEF=∠DFE.∴AE∥DF.
∴以A、F、D、E为顶点的四边形是平行四边形.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图所示,池塘边有块长为20m,宽为10m的长方形土地,现在将其余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用含x的式子表示:
(1)菜地的长a= m,菜地的宽b= m;菜地的周长C= m;
(2)求当x=1m时,菜地的周长C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于
在第一象限的图象交于 ![]() 点,过
点,过 ![]() 点作
点作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ,已知
,已知 ![]() 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且
不重合),且 ![]() 点的横坐标为1,在
点的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是BC,AB, AC的中点,则下列四个判断中不一定正确的是( )
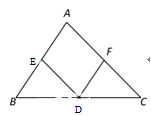
A. 四边形AEDF一定是平行四边形
B. 若∠A=90°,则四边形AEDF是矩形
C. 若AD平分∠A,则四边形AEDF是正方形
D. 若AD⊥BC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在解方程组![]() 时,采用了一种“整体代换”解法:
时,采用了一种“整体代换”解法:
解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5......③
把方程①带入③得:2×3+y=5,
y=-1
y=-1代入①得x=4
∴方程组的解为![]()
请你解决以下问题:
(1)参考小明的“整体代换”法解方程组![]()
(2)已知x,y满足方程组:![]()
(i)求![]() 的值;
的值;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于 ![]() ,记为
,记为 ![]() ,这个数
,这个数 ![]() 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为 ![]() (
( ![]() 为实数),
为实数), ![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: ![]()
(1)填空: ![]() = ,
= , ![]() = .
= .
(2)填空:① ![]() ; ②
; ② ![]() .
.
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求 ![]() 的值.
的值.
(4)试一试:请利用以前学习的有关知识将 ![]() 化简成
化简成 ![]() 的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com