
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
【答案】(1)甲、乙两组工作一天,商店各应付300元和140元;(2)单独请乙组需要的费用少;(3)甲乙合作施工更有利于商店.
【解析】
(1)设甲组单独工作一天商店应付x元,乙组单独工作一天商店应付y元,根据总费用与时间的关系建立方程组求出其解即可;
(2)由甲乙单独完成需要的时间,再结合(1)求出甲、乙两组单独完成的费用进行比较就可以得出结论;
(3)先比较甲、乙单独装修的时间和费用谁对商店经营有利,再比较合作装修与甲单独装修对商店的有利经营情况,从而可以得出结论.
解:(1)设:甲组工作一天商店应付x元,乙组工作一天商店付y元.
由题意得:![]()
解得:![]()
答:甲、乙两组工作一天,商店各应付300元和140元
(2)单独请甲组需要的费用:300×12=3600元.
单独请乙组需要的费用:24×140=3360元.
答:单独请乙组需要的费用少.
(3)请两组同时装修,理由:
甲单独做,需费用3600元,少赢利200×12=2400元,相当于损失600000元;
乙单独做,需费用3360元,少赢利200X24=4800元,相当于损失8160元;
甲乙合作,需费用3520元,少赢利200×8=1600元,相当于损失5120元;
因为5120<6000<8160,所以甲乙合作损失费用最少,
答:甲乙合作施工更有利于商店.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(2,﹣1)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,3),连接AB.
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是BC,AB, AC的中点,则下列四个判断中不一定正确的是( )
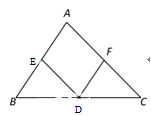
A. 四边形AEDF一定是平行四边形
B. 若∠A=90°,则四边形AEDF是矩形
C. 若AD平分∠A,则四边形AEDF是正方形
D. 若AD⊥BC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在解方程组![]() 时,采用了一种“整体代换”解法:
时,采用了一种“整体代换”解法:
解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5......③
把方程①带入③得:2×3+y=5,
y=-1
y=-1代入①得x=4
∴方程组的解为![]()
请你解决以下问题:
(1)参考小明的“整体代换”法解方程组![]()
(2)已知x,y满足方程组:![]()
(i)求![]() 的值;
的值;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)




(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+8分别交两轴于点A、B,点C的横坐标为4,点D在线段OA上,且AD=7.
(1)求直线CD的解析式;
(2)P为直线CD上一点,若△PAB面积为20,求P的坐标;
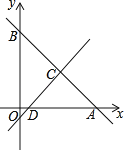
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索:你能求(x﹣1)(x2019+x2018+x2017+……+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
(1)(x﹣1)(x+1)=x2﹣1;
(2)(x﹣1)(x2+x+1)=x3﹣1;
(3)(x﹣1)(x3+x2+x+1)=x4﹣1;
……
由此我们可以得到:(x﹣1)(x2019+x2018+x2017+……+x+1)= ;请你利用上面的结论,完成下面两题的计算:
(1)32019+32018+32017+……+3+1;
(2)(﹣2)50+(﹣2)49+(﹣2)48+……+(﹣2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com