
【题目】如图,在平面直角坐标系中,抛物线y=ax-4ax交x轴于点A,直线y= ![]() x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
x+3与x轴交于点B,与y轴交于点C,与抛物线交于点D,E(点D在点E的右侧).
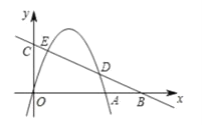
(1)求点A,B,C的坐标.
(2)当点D为BC的中点时,求a的值.
(3)若设抛物线的顶点为点M,点M关于直线BC的对称点为N, 当点N落在△BOC的内部时,求a的取值范围.
【答案】(1)A(4,0),B(6,0),C(0,3);(2)a=![]() ;(3)
;(3)![]() <a<
<a<![]()
【解析】
(1)利用抛物线的解析式求出点A的坐标,再利用一次函数解析式,由y=0求出对应的x的值,由x=0求出对应的y的值,即可得到点B,C的坐标;
(2)利用中点坐标求出点D的坐标,再将点D的坐标代入抛物线的解析式求出a的值;(3)将函数解析式转化为顶点式,可得到顶点M的坐标,再分情况讨论:当N恰好落存OC上时,作MH⊥y轴,连接CM,易证△HMN∽△OCB,利用已知求出a的值;当N落在x轴上时,可以求得N不在OB内(N不可能在线段OB上);当N落在BC上时,则M也在BC上,易求出a的值,即可得到a的取值范围.
(1)解:∵抛物线y=ax2-4ax交x轴于点A,
∴当y=0时,![]() ,
,
解得![]() ,
,
∴A(4,0),
∵直线y=![]() x+3与x轴交于点B,与y轴交于点C,
x+3与x轴交于点B,与y轴交于点C,
∴当y=0时得x=6,当x=0时得y=3,
∴B(6,0),C(0,3).
(2)解:∵点D为BC的中点,
∴点D的坐标为(3,![]() ),
),
把(3,![]() )代入y=ax2-4ax得a=
)代入y=ax2-4ax得a=![]() ,
,
(3)解:由y=ax2-4ax=a(x-2)2-4a,∴M(2,-4a) ,
当N恰好落在OC上时,作MH⊥y轴,连接CM,
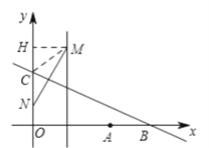
∴MN⊥BC,
∴∠MNH+∠OCB=90°,
∵∠OCB+∠OBC=90°,
∴∠MNH=∠OBC,
∵∠MHN=∠COB=90°,
∴△HMN∽△OCB,
∴ ![]() ,
,
∵HM=2,OC=3,OB=6,
∴HN=4,
∵CM=CN,
∴在Rt△HCM中利用勾股定理,得CN=CM=![]() ,CH=
,CH=![]() ,
,
∴OH=![]() ,
,
∴-4a=![]() ,
,
∴a=![]() ;
;
当N落在x轴上时,可以求得N不在OB内(N不可能在线段OB上);
当N落在BC上时,则M也在BC上,此时a=![]() .
.
∴ ![]() <a<
<a<![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点P(x,y)经过某种变换后到点![]() (-y+1,x+2),我们把点
(-y+1,x+2),我们把点![]() (-y+1,x+2)叫做点P(x,y)的终结点,已知点
(-y+1,x+2)叫做点P(x,y)的终结点,已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() 若点
若点![]() 的坐标为(2,0),则点
的坐标为(2,0),则点![]() 的坐标为_______
的坐标为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一方有难,八方支援”是中华民族的传统美德.2月20日13时25分,山西第12批支援武汉医疗队整装出发,在抗击新冠病毒战役中,我省支援湖北医疗队共1500多人奔赴武汉.其中小丽、小王和三个同事共五人直接派往一线某医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到发热门诊,请你利用所学知识完成下列问题.

(1)小丽被派往急诊科的概率是______;
(2)若正好抽出她们一同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
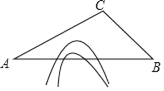
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
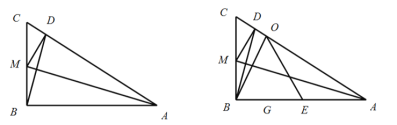
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
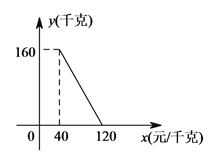
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
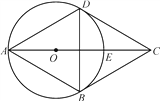
【题目】已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
(1)判断⊙O与BC的位置关系,并说明理由;
(2)若CE=2,求⊙O的半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com