
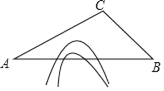
����Ŀ�������й����õĿ��ٷ�չ�Լ��Ƽ�ˮƽ�ķ�����ߣ��й�������Ѹ�����𣮸������������ʱ�վ��룬�ı������ǵij��з�ʽ����ͼ��A��B���ر���ɽ�������A�ص�B����Ҫ����C�أ�����ͨ��ɽ����������A��B���ص�ֱ��������������̴�A�ص�B�ص�·�̣���֪����CAB=30�㣬��CBA=45�㣬AC=640�����������ͨ�����ͨǰ��ȣ���A�ص�B�ص�·�̽�Լ���̶��ٹ�����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������ͼ��P��-2��3����
(1)��˷����������Ľ���ʽ��
(2)��A(2��-3)��B(3��2)�Ƿ������������ͼ���ϣ�
(3)���������ͼ��λ����Щ���ޣ�����ֵy���Ա���x�ļ�С��α仯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
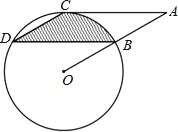
����Ŀ����ͼ����B��C��D���ڡ�O�ϣ�����C��AC��BD��OB�ӳ����ڵ�A������CD���ҡ�CDB=��OBD=30����DB=![]() cm��
cm��
��1����֤��AC�ǡ�O�����ߣ�
��2��������CD��BD�뻡BC��Χ�ɵ���Ӱ���ֵ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=![]() ��nΪ��������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB=2OA=3OD=12��
��nΪ��������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB=2OA=3OD=12��
��1����һ�κ����뷴���������Ľ���ʽ��
��2����������ͼ�����һ������ΪE������CDE�������
��3��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ı���ACED����ƽ���ı��Σ���RΪDE���е㣬BR�ֱ�AC��CD�ڵ�P��Q��
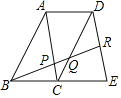
��1����֤����ABP�ס�DQR��
��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
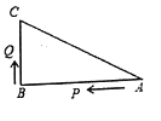
����Ŀ����ͼ��ʾ����֪![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ı��ϵ��������㣬���е�
�ı��ϵ��������㣬���е�![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����˶������ٶ�Ϊÿ��
�����˶������ٶ�Ϊÿ��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����˶������ٶ�Ϊÿ��
�����˶������ٶ�Ϊÿ��![]() ������ͬʱ�������������ʱ��Ϊ
������ͬʱ�������������ʱ��Ϊ![]() ��
��
��1����![]() ____________
____________![]() ��
��
��2����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() �ڱ�
�ڱ�![]() �Ĵ�ֱƽ�����ϣ���ʱ
�Ĵ�ֱƽ�����ϣ���ʱ![]() _________?
_________?
��3������![]() �ڱ�
�ڱ�![]() ���˶�ʱ��ֱ��д��ʹ
���˶�ʱ��ֱ��д��ʹ![]() ��Ϊ���������ε��˶�ʱ����
��Ϊ���������ε��˶�ʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC����![]() ����D=120����������ABCD�����Ϊ�� ��
����D=120����������ABCD������� ��
A.![]() B.54C.36D.
B.54C.36D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
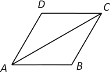
����Ŀ���������н�����ͼ����ʾ��ƽ��ֱ������ϵ����������![]() ��
��![]() ��
��![]() ��λ����ͼ�����ǵ�����ֱ�Ϊ
��λ����ͼ�����ǵ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
(1)��ͼ�ڣ���������![]() ��ʹ
��ʹ![]() ��
��![]() ��
��![]() ��
��![]() Ϊ�˵��������β���ӵ��߶�Χ�ɵ�ͼ�γ�Ϊ��Գ�ͼ�Σ�����ͼ�л�����ͼ�εĶԳ��
Ϊ�˵��������β���ӵ��߶�Χ�ɵ�ͼ�γ�Ϊ��Գ�ͼ�Σ�����ͼ�л�����ͼ�εĶԳ��
(2)���������λ������һ������![]() ��ʹ
��ʹ![]() ��
��![]() ��
��![]() ��
��![]() Ϊ�˵����β���ӵ������߶ι���һ����Գ�ͼ�Σ���ֱ��д����
Ϊ�˵����β���ӵ������߶ι���һ����Գ�ͼ�Σ���ֱ��д����![]() �����ꡣ(дɽ2������)
�����ꡣ(дɽ2������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ڸ����Ķ��κ���y=a��x��h��2+k��a��0���������һ�κ���Ϊy=a��x��h��+k�����磺���κ���y=2��x+1��2��3�İ���һ�κ���Ϊy=2��x+1����3����y=2x��1��
��1����֪���κ���y=��x��1��2��4���������һ�κ����ı���ʽΪ_____��
��2����˵�����κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
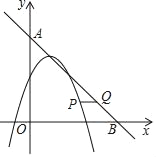
��3����ͼ�����κ���y=m��x��1��2��4m��m��0���İ���һ�κ�����ͼ����x�ᡢy��ֱ��ڵ�B��A����������ͼ��Ľ���ĺ�����ֱ�Ϊ1��2���ڡ�AOB�ڲ��Ķ��κ���y=m��x��1��2��4m��ͼ������һ����P������P��x���ƽ�����������һ�κ�����ͼ���ڵ�Q�����P�ĺ�����Ϊn��ֱ��д���߶�PQ�ij�Ϊ![]() ʱn��ֵ��
ʱn��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com