
����Ŀ�����壺���ڸ����Ķ��κ���y=a��x��h��2+k��a��0���������һ�κ���Ϊy=a��x��h��+k�����磺���κ���y=2��x+1��2��3�İ���һ�κ���Ϊy=2��x+1����3����y=2x��1��
��1����֪���κ���y=��x��1��2��4���������һ�κ����ı���ʽΪ_____��
��2����˵�����κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
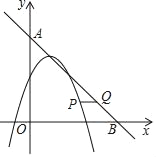
��3����ͼ�����κ���y=m��x��1��2��4m��m��0���İ���һ�κ�����ͼ����x�ᡢy��ֱ��ڵ�B��A����������ͼ��Ľ���ĺ�����ֱ�Ϊ1��2���ڡ�AOB�ڲ��Ķ��κ���y=m��x��1��2��4m��ͼ������һ����P������P��x���ƽ�����������һ�κ�����ͼ���ڵ�Q�����P�ĺ�����Ϊn��ֱ��д���߶�PQ�ij�Ϊ![]() ʱn��ֵ��
ʱn��ֵ��
���𰸡�y=x��5
����������������1�����ݶ��壬ֱ�ӱ��εõ�����һ�κ����Ľ���ʽ��
��2��������㣬���������������ʽ������⣻
��3����������õ�������������ʽ������P������꣬�����ʾ�������꣬Ȼ��ͨ��PQ��x���ƽ�й�ϵ�����Q������꣬��PQ�ij��з�����⼴��.
��⣺��1���߶��κ���y=��x��1��2��4��
�������һ�κ����ı���ʽΪy=��x��1����4=x��5��
�ʴ�Ϊy=x��5��
��2���߶��κ���y=��x��1��2��4��
�ඥ������Ϊ��1����4����
�߶��κ���y=��x��1��2��4��
�������һ�κ����ı���ʽΪy=x��5��
�൱x=1ʱ��y=1��5=��4��
�ࣨ1����4����ֱ��y=x��5�ϣ�
�������κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
��3���߶��κ���y=m��x��1��2��4m��
�������һ�κ���Ϊy=m��x��1����4m=mx��5m��
��P��ĺ�����Ϊn����n��2����
��P��������Ϊm��n��1��2��4m��
����P��n��m��n��1��2��4m����
��PQ��x�ᣬ
��Q����n��1��2+1��m��n��1��2��4m����
��PQ=��n��1��2+1��n��
���߶�PQ�ij�Ϊ![]() ��
��
�ࣨn��1��2+1��n=![]() ��
��
��n=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
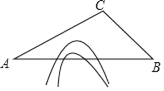
����Ŀ�������й����õĿ��ٷ�չ�Լ��Ƽ�ˮƽ�ķ�����ߣ��й�������Ѹ�����𣮸������������ʱ�վ��룬�ı������ǵij��з�ʽ����ͼ��A��B���ر���ɽ�������A�ص�B����Ҫ����C�أ�����ͨ��ɽ����������A��B���ص�ֱ��������������̴�A�ص�B�ص�·�̣���֪����CAB=30�㣬��CBA=45�㣬AC=640�����������ͨ�����ͨǰ��ȣ���A�ص�B�ص�·�̽�Լ���̶��ٹ�����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
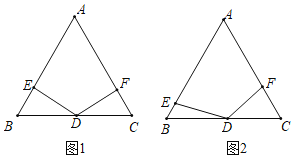
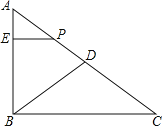
����Ŀ���ڵȱ�������ABC�У���D��BC���е㣬��E��F�ֱ��DZ�AB��AC�����߶�AB��AC�Ķ˵㣩�ϵĶ��㣬�ҡ�EDF=120����С����С�۶����ͼ��չ�������о���
�����̽��
��1����ͼ1��С�����֣�����DEB=90��ʱ��BE+CF=nAB����n��ֵΪ______��
������̽��
��2����ͼ2���ڵ�E��F���˶������У�С�۷���������Ȥ�Ľ��ۣ�
��DEʼ�յ���DF����BE��CF�ĺ�ʼ�ղ��䣻����ѡ������һ�����ۼ���֤����
�ɹ�����
��3�����߳�AB=4���ڵ�E��F���˶������У����ı���DEAF���ܳ�ΪL��L=DE+EA+AF+FD�����ܳ�L�ı仯��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������40Ԫ����Ʒ��50Ԫ���ۣ�������500������֪������Ʒÿ�Ǽ�1Ԫ���ͻ�������10����Ϊ����8000Ԫ�������ۼ�Ӧ��Ϊ���٣���ʱӦ�������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Զ������Ĺ�·l����һ���վA���ڹ۲��B����ƫ��53�������վһ������Ա��ס����۲��B�ľ���Ϊ7![]() km��λ�ڵ�B��ƫ��76������ĵ�C����������Ա�ҵ����վ�ľ���AC�����ο����ݣ�sin76����
km��λ�ڵ�B��ƫ��76������ĵ�C����������Ա�ҵ����վ�ľ���AC�����ο����ݣ�sin76����![]() ��cos76����
��cos76����![]() ��tan 76����4��sin53����
��tan 76����4��sin53����![]() ��tan53����
��tan53����![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() �ǽ�ƽ���ߣ�
�ǽ�ƽ���ߣ�![]() ��
��
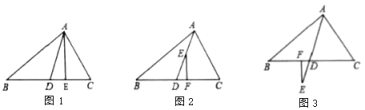
��1����ͼ1��![]() �Ǹߣ�
�Ǹߣ�![]() ��
��![]() ����
����![]()
![]() ��ֱ��д�����ۣ�����д������̣���
��ֱ��д�����ۣ�����д������̣���
��2����ͼ2����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ����̽��
����̽��![]() ��
��![]() ��
��![]() ֮���������ϵ��д�����̽�����۲�֤����
֮���������ϵ��д�����̽�����۲�֤����
��3����ͼ3����![]() ��
��![]() ���ӳ����ϣ�
���ӳ����ϣ�![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ֮���������ϵ�� ����ֱ��д�����ۣ�����֤����.
֮���������ϵ�� ����ֱ��д�����ۣ�����֤����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
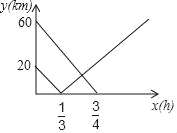
����Ŀ��������A��B���еĹ�·֮����һ������C�����������A��ʻ�����C��������B��ʻ��A�У�����ͬʱ����������ʻ��ͼ���߶Ρ����߷ֱ��ʾ������͡�����������C��·��y��km�������ʱ��x��h��֮��ĺ�����ϵͼ��
��1��ֱ��д������A��B���й�·��·���Լ�������B�е���A������ʱ�䣮
��2���������͵�����C��·��y��km�������ʱ��x��h��֮��ĺ�����ϵʽ��
��3��������������������ص�����C��·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC��90����AC��15cm��BC��12cm����D���߶�AC���е㣬����P��A��D��B��C���յ�C�������ٶ�Ϊ5cm/s������P�����A��B�غ�ʱ����PE��AB���߶�AB�ڵ�E�����P���˶�ʱ��Ϊt��s������APE�����ΪS��cm2����
��1��д���߶�AB�ij���
��2������P���߶�BD��ʱ����PE�ij����ú�t��ʽ�ӱ�ʾ����
��3������P��A��D��B�˶�ʱ���ú�t�Ĵ���ʽ��ʾS��
��4����E����ֱ��AP�ĶԳƵ�ΪE��������E��������ABC���ڲ�ʱ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ![]() ������ʽ�ֽ�Ĺ��̣�
������ʽ�ֽ�Ĺ��̣�
�⣺��![]() ��
��
ԭʽ![]() ����һ����
����һ����
![]() ���ڶ�����
���ڶ�����
![]() ����������
����������
![]() �����IJ���
�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_____________��
A����ȡ����ʽ B��ƽ���ʽ
C�������͵���ȫƽ����ʽ D�����������ȫƽ����ʽ
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿ�__________������ס������ס���
�������ף���ֱ��д����ʽ�ֽ�������_____________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com