
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
问题初探:
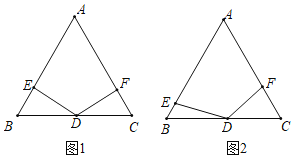
(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为______;
问题再探:
(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用
(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是______.
【答案】(1)![]() ;(2)BE与CF的和始终不变,见解析;(3)
;(2)BE与CF的和始终不变,见解析;(3)![]()
【解析】
(1)先利用等边三角形判断出BD=CD=![]() AB,进而判断出BE=
AB,进而判断出BE=![]() BD,再判断出∠DFC=90°,得出CF=
BD,再判断出∠DFC=90°,得出CF=![]() CD,即可得出结论;
CD,即可得出结论;
(2)①构造出△EDG≌△FDH(ASA),得出DE=DF,即可得出结论;
②由(1)知,BG+CH=![]() AB,由①知,△EDG≌△FDH(ASA),得出EG=FH,即可得出结论;
AB,由①知,△EDG≌△FDH(ASA),得出EG=FH,即可得出结论;
(3)由(1)(2)判断出L=2DE+6,再判断出DE⊥AB时,L最小,点F和点C重合时,DE最大,即可得出结论.
解:(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∵点D是BC的中点,
∴BD=CD=![]() BC=
BC=![]() AB,
AB,
∵∠DEB=90°,
∴∠BDE=90°-∠B=30°,
在Rt△BDE中,BE=![]() BD,
BD,
∵∠EDF=120°,∠BDE=30°,
∴∠CDF=180°-∠BDE-∠EDF=30°,
∵∠C=60°,
∴∠DFC=90°,
在Rt△CFD中,CF=![]() CD,
CD,
∴BE+CF=![]() BD+
BD+![]() CD=
CD=![]() BC=
BC=![]() AB,
AB,
∵BE+CF=nAB,
∴n=![]() ,
,
故答案为![]() ;
;
(2)如图2
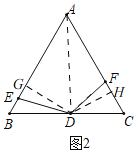
①过点D作DG⊥AB于G,DH⊥AC于H,
∴∠DGB=∠AGD=∠CFD=∠AHF=90°,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠GDH=360°-∠AGD-∠AHD-∠A=120°,
∵∠EDF=120°,
∴∠EDG=∠FDH,
∵△ABC是等边三角形,且D是BC的中点,
∴∠BAD=∠CAD,
∵DG⊥AB,DH⊥AC,
∴DG=DH,
在△EDG和△FDH中,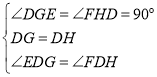 ,
,
∴△EDG≌△FDH(ASA),
∴DE=DF,
即:DE始终等于DF;
②同(1)的方法得,BG+CH=![]() AB,
AB,
由①知,△EDG≌△FDH(ASA),
∴EG=FH,
∴BE+CF=BG-EG+CH+FH=BG+CH=![]() AB,
AB,
∴BE与CF的和始终不变
(3)由(2)知,DE=DF,BE+CF=![]() AB,
AB,
∵AB=4,
∴BE+CF=2,
∴四边形DEAF的周长为L=DE+EA+AF+FD
=DE+AB-BE+AC-CF+DF
=DE+AB-BE+AB+DE
=2DE+2AB-(BE+CF)
=2DE+2×4-2
=2DE+6,
∴DE最大时,L最大,DE最小时,L最小,
当DE⊥AB时,DE最小,
由(1)知,BG=![]() BD=1,
BD=1,
∴DE最小=![]() BG=
BG=![]() ,
,
∴L最小=2![]() +6,
+6,
当点F和点C重合时,DE最大,此时,∠BDE=180°-∠EDF=120°=60°,
∵∠B=60°,
∴∠B=∠BDE=∠BED=60°,
∴△BDE是等边三角形,
∴DE=BD=![]() AB=2,
AB=2,
即:L最大=2×2+6=10,
∴周长L的变化范围是2![]() ≤L≤10,
≤L≤10,
故答案为2![]() ≤L≤10.
≤L≤10.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
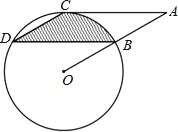
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
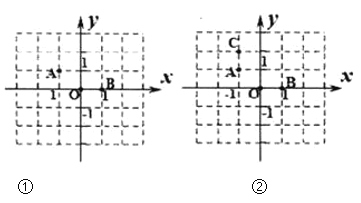
【题目】在棋盘中建立如图①所示的平面直角坐标系,二颗棋子![]() 、
、![]() 、
、![]() 的位置如图,它们的坐标分别为
的位置如图,它们的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)如图②,添加棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 为端点的四条首尾连接的线段围成的图形成为轴对称图形,请在图中画出该图形的对称轴;
为端点的四条首尾连接的线段围成的图形成为轴对称图形,请在图中画出该图形的对称轴;
(2)在其它格点位置添加一颗棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 为端点的首尾连接的四条线段构成一个轴对称图形,请直接写出点
为端点的首尾连接的四条线段构成一个轴对称图形,请直接写出点![]() 的坐标。(写山2个即可)
的坐标。(写山2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
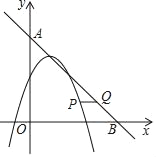
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )

A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com