
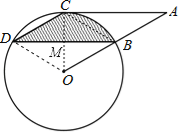
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
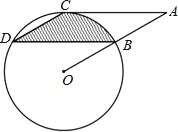
【答案】(1)证明见解析;(2)6πcm2.
【解析】试题分析:连接BC,OD,OC,设OC与BD交于点M.(1)求出∠COB的度数,求出∠A的度数,根据三角形的内角和定理求出∠OCA的度数,根据切线的判定推出即可;
(2)证明△CDM≌△OBM,从而得到S阴影=S扇形BOC.
试题解析:如图,连接BC,OD,OC,设OC与BD交于点M.
(1)根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,∵AC∥BD,∴∠A=∠OBD=30°,∴∠OCA=180°﹣30°﹣60°=90°,即OC⊥AC,∵OC为半径,∴AC是⊙O的切线;
(2)由(1)知,AC为⊙O的切线,∴OC⊥AC.∵AC∥BD,∴OC⊥BD.由垂径定理可知,MD=MB=![]() BD=3
BD=3![]() .在Rt△OBM中,∠COB=60°,OB=
.在Rt△OBM中,∠COB=60°,OB=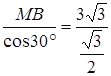 =6.
=6.
在△CDM与△OBM中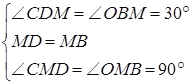 ,∴△CDM≌△OBM(ASA),∴S△CDM=S△OBM
,∴△CDM≌△OBM(ASA),∴S△CDM=S△OBM
∴阴影部分的面积S阴影=S扇形BOC=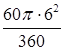 =6π(cm2).
=6π(cm2).


科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
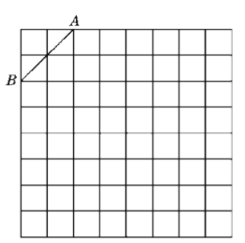
(1)请在网格中建立平面直角坐标系,使点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)在第二象限内的格点上找一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数,画出
为底的等腰三角形,且腰长是无理数,画出![]() ,则点
,则点![]() 的坐标是 ,
的坐标是 ,![]() 的周长是 (结果保留根号);
的周长是 (结果保留根号);
(3)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
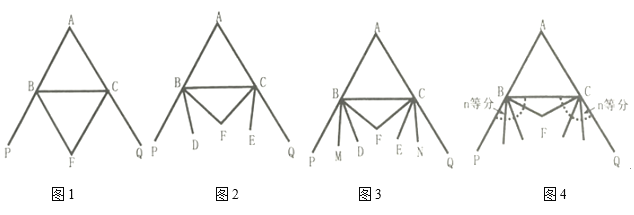
【题目】(1)如图1,已知![]() ,
,![]() 平分外角
平分外角![]() ,
,![]() 平分外角
平分外角![]() .直接写出
.直接写出![]() 和
和![]() 的数量关系,不必证明;
的数量关系,不必证明;
(2)如图2,已知![]() ,
,![]() 和
和![]() 三等分外角
三等分外角![]() ,
,![]() 和
和![]() 三等分外角
三等分外角![]() .试确定
.试确定![]() 和
和![]() 的数量关系,并证明你的猜想;(不写证明依据)
的数量关系,并证明你的猜想;(不写证明依据)
(3)如图3,已知![]() ,
,![]() 、
、![]() 和
和![]() 四等分外角
四等分外角![]() ,
,![]() 、
、![]() 和
和![]() 四等分外角
四等分外角![]() .试确定
.试确定![]() 和
和![]() 的数量关系,并证明你的猜想;(不写证明依据)
的数量关系,并证明你的猜想;(不写证明依据)
(4)如图4,已知![]() ,将外角
,将外角![]() 进行
进行![]() 分,
分,![]() 是临近
是临近![]() 边的等分线,将外角
边的等分线,将外角![]() 进行
进行![]() 等分,
等分,![]() 是临近
是临近![]() 边的等分线,请直接写出
边的等分线,请直接写出![]() 和
和![]() 的数量关系,不必证明.
的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
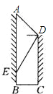
【题目】如图,为响应人民政府“形象重于生命”的号召,规划部门在甲建筑物的顶部![]() 点测得条幅顶端
点测得条幅顶端![]() 的仰角为
的仰角为![]() ,测得条幅底端的俯角为
,测得条幅底端的俯角为![]() ,已知条幅长
,已知条幅长![]() ,则底部不能直接到达的甲、乙两建筑物之间的水平距离
,则底部不能直接到达的甲、乙两建筑物之间的水平距离![]() 的长为________
的长为________![]() .(答案可带根号)
.(答案可带根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
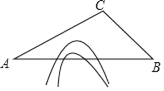
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
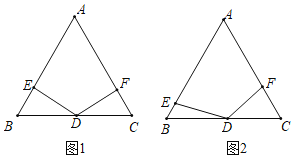
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
问题初探:
(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为______;
问题再探:
(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用
(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com