
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

【答案】(1)抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2
x+2
(2)存在,P1(![]() ,4),P2(
,4),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )
)
(3)当点E运动到(2,1)时,四边形CDBF的面积最大,S四边形CDBF的面积最大=![]() .
.
【解析】
试题(1)将点A、C的坐标分别代入可得二元一次方程组,解方程组即可得出m、n的值;
(2)根据二次函数的解析式可得对称轴方程,由勾股定理求出CD的值,以点C为圆心,CD为半径作弧交对称轴于P1;以点D为圆心CD为半径作圆交对称轴于点P2,P3;作CH垂直于对称轴与点H,由等腰三角形的性质及勾股定理就可以求出结论;
(3)由二次函数的解析式可求出B点的坐标,从而可求出BC的解析式,从而可设设E点的坐标,进而可表示出F的坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式,由二次函数的性质就可以求出结论.
试题解析:(1)∵抛物线y=﹣![]() x2+mx+n经过A(﹣1,0),C(0,2).
x2+mx+n经过A(﹣1,0),C(0,2).
解得: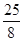 ,
,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵y=﹣![]() x2+
x2+![]() x+2,
x+2,
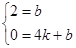
∴y=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴抛物线的对称轴是x=![]() .
.
∴OD=![]() .
.
∵C(0,2),
∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=![]() .
.
∵△CDP是以CD为腰的等腰三角形,
∴CP1=CP2=CP3=CD.
作CH⊥x轴于H,
∴HP1=HD=2,
∴DP1=4.
∴P1(![]() ,4),P2(
,4),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() );
);
(3)当y=0时,0=﹣![]() x2+
x2+![]() x+2
x+2
∴x1=﹣1,x2=4,
∴B(4,0).
设直线BC的解析式为y=kx+b,由图象,得
![]() ,
,
解得: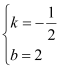 ,
,
∴直线BC的解析式为:y=﹣![]() x+2.
x+2.
如图2,过点C作CM⊥EF于M,设E(a,﹣![]() a+2),F(a,﹣
a+2),F(a,﹣![]() a2+
a2+![]() a+2),
a+2),
∴EF=﹣![]() a2+
a2+![]() a+2﹣(﹣
a+2﹣(﹣![]() a+2)=﹣
a+2)=﹣![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵S四边形CDBF=S△BCD+S△CEF+S△BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN,
EFBN,
=![]() +
+![]() a(﹣
a(﹣![]() a2+2a)+
a2+2a)+![]() (4﹣a)(﹣
(4﹣a)(﹣![]() a2+2a),
a2+2a),
=﹣a2+4a+![]() (0≤x≤4).
(0≤x≤4).
=﹣(a﹣2)2+![]()
∴a=2时,S四边形CDBF的面积最大=![]() ,
,
∴E(2,1).



科目:初中数学 来源: 题型:
【题目】据医学研究,使用某种抗生素治疗心肌炎,人体内每毫升血液中的含药量不少于4微克时,治疗有效.如果一患者按规定剂量服用这种抗生素,服用后每毫升血液中的含药量![]() (微克)与服用后的时间
(微克)与服用后的时间![]() (小时)之间的函数关系如图所示:
(小时)之间的函数关系如图所示:
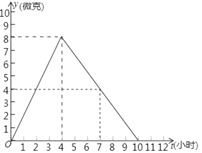
(1)如果上午8时服用该药物,到 时该药物的浓度达到最大值 微克/毫升;
(2)根据图象求出从服用药物起到药物浓度最高时y与t之间的函数解析式;
(3)如果上午8时服用该药物,到 时该药物开始有效,有效时间一共是 小时;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角? (填“是”或“不是”).
小丽经过三次折叠发现了∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
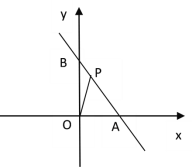
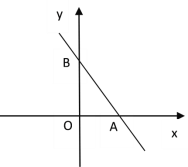
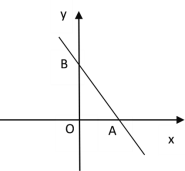
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒:
秒:
(1)![]() ________
________![]() ;(用的代数式表示)
;(用的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ;
;
(3)当点![]() 从点
从点![]() 开始运动,同时,点
开始运动,同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得
值,使得![]() 与
与![]() 全等?若存在,请求出
全等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com