
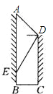
【题目】如图,为响应人民政府“形象重于生命”的号召,规划部门在甲建筑物的顶部![]() 点测得条幅顶端
点测得条幅顶端![]() 的仰角为
的仰角为![]() ,测得条幅底端的俯角为
,测得条幅底端的俯角为![]() ,已知条幅长
,已知条幅长![]() ,则底部不能直接到达的甲、乙两建筑物之间的水平距离
,则底部不能直接到达的甲、乙两建筑物之间的水平距离![]() 的长为________
的长为________![]() .(答案可带根号)
.(答案可带根号)
科目:初中数学 来源: 题型:
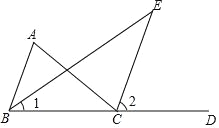
【题目】如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E,以下是小明的证明过程,请在括号里填写理由.
证明:∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知)
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(_________)
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知)
∴∠ACD=2∠2,∠ABC=2∠1(_______)
∴∠A=2∠2﹣2∠1(_________)
=2(∠2﹣∠1)(_________)
=2∠E(等量代换)
(2)如果∠A=∠ABC,求证:CE∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
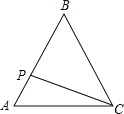
【题目】已知AD为⊙O的直径,BC为⊙O的切线,切点为M,分别过A,D两点作BC的垂线,垂足分别为B,C,AD的延长线与BC相交于点E.
(1)求证:△ABM∽△MCD;
(2)若AD=8,AB=5,求ME的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(s),y=PC2,则y关于x的函数的图像大致为 ( )
A. 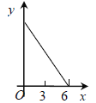 B.
B. 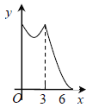 C.
C. 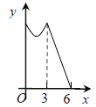 D.
D. 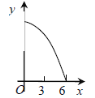
查看答案和解析>>
科目:初中数学 来源: 题型:
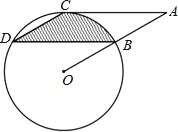
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 的边上的两个动点,其中点
的边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为![]() .
.
(1)则![]() ____________
____________![]() ;
;
(2)当![]() 为何值时,点
为何值时,点![]() 在边
在边![]() 的垂直平分线上?此时
的垂直平分线上?此时![]() _________?
_________?
(3)当点![]() 在边
在边![]() 上运动时,直接写出使
上运动时,直接写出使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
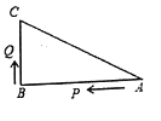
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com