
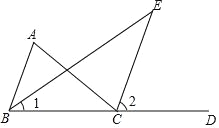
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘФЪЎчABCЦРЈ¬CEКЗНвҪЗЎПACDөДЖҪ·ЦПЯЈ¬BEКЗЎПABCөДЖҪ·ЦПЯЈ®
(1)ЗуЦӨЈәЎПAЈҪ2ЎПEЈ¬ТФПВКЗРЎГчөДЦӨГч№эіМЈ¬ЗлФЪАЁәЕАпМоРҙАнУЙЈ®
ЦӨГчЈәЎЯЎПACDКЗЎчABCөДТ»ёцНвҪЗЈ¬ЎП2КЗЎчBCEөДТ»ёцНвҪЗЈ¬(ТСЦӘ)
ЎаЎПACDЈҪЎПABC+ЎПAЈ¬ЎП2ЈҪЎП1+ЎПE(_________)
ЎаЎПAЈҪЎПACD©ҒЎПABCЈ¬ЎПEЈҪЎП2©ҒЎП1(өИКҪөДРФЦК)
ЎЯCEКЗНвҪЗЎПACDөДЖҪ·ЦПЯЈ¬BEКЗЎПABCөДЖҪ·ЦПЯ(ТСЦӘ)
ЎаЎПACDЈҪ2ЎП2Ј¬ЎПABCЈҪ2ЎП1(_______)
ЎаЎПAЈҪ2ЎП2©Ғ2ЎП1(_________)
ЈҪ2(ЎП2©ҒЎП1)(_________)
ЈҪ2ЎПE(өИБҝҙъ»»)
(2)Из№ыЎПAЈҪЎПABCЈ¬ЗуЦӨЈәCEЎОABЈ®
Ўҫҙр°ёЎҝ(1)јыҪвОцЈ»(2)ЦӨГчјыҪвОц.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭҪЗЖҪ·ЦПЯөДРФЦКТФј°ИэҪЗРОНвҪЗөДРФЦКјҙҝЙЗуЦӨЈ»
ЈЁ2Ј©УЙЈЁ1Ј©ҝЙЦӘЈәЎПAЈҪ2ЎПEЈ¬УЙУЪЎПAЈҪЎПABCЈ¬ЎПABCЈҪ2ЎПABEЈ¬ЛщТФЎПEЈҪЎПABEЈ¬ҙУ¶шҝЙЦӨABЎОCEЈ®
ҪвЈә(1)ЎЯЎПACDКЗЎчABCөДТ»ёцНвҪЗЈ¬ЎП2КЗЎчBCEөДТ»ёцНвҪЗЈ¬(ТСЦӘ)Ј¬
ЎаЎПACDЈҪЎПABC+ЎПAЈ¬ЎП2ЈҪЎП1+ЎПE(ИэҪЗРОНвҪЗөДРФЦК)Ј¬
ЎаЎПAЈҪЎПACD©ҒЎПABCЈ¬ЎПEЈҪЎП2©ҒЎП1(өИКҪөДРФЦК)Ј¬
ЎЯCEКЗНвҪЗЎПACDөДЖҪ·ЦПЯЈ¬BEКЗЎПABCөДЖҪ·ЦПЯ(ТСЦӘ)Ј¬
ЎаЎПACDЈҪ2ЎП2Ј¬ЎПABCЈҪ2ЎП1(ҪЗЖҪ·ЦПЯөДРФЦК )Ј¬
ЎаЎПAЈҪ2ЎП2©Ғ2ЎП1( өИБҝҙъ»»)Ј¬
ЈҪ2(ЎП2©ҒЎП1)(МбИЎ№«ТтКэ)Ј¬
ЈҪ2ЎПE(өИБҝҙъ»»)Ј»
(2)УЙ(1)ҝЙЦӘЈәЎПAЈҪ2ЎПE
ЎЯЎПAЈҪЎПABCЈ¬ЎПABCЈҪ2ЎПABEЈ¬
Ўа2ЎПEЈҪ2ЎПABEЈ¬
јҙЎПEЈҪЎПABEЈ¬
ЎаABЎОCEЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬ТСЦӘ
Ј¬ТСЦӘ![]() Ј¬
Ј¬![]() Ул
Ул![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() Ј¬
Ј¬![]() Ул
Ул![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() Ј¬
Ј¬![]() Ул
Ул![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() .
.
ЈЁ1Ј©ИзНјЈ¬№ЫІмІўІВПл![]() әН
әН![]() УРФхСщөДКэБҝ№ШПөЈҝІўЛөГчАнУЙ.
УРФхСщөДКэБҝ№ШПөЈҝІўЛөГчАнУЙ.
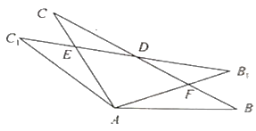
ЈЁ2Ј©уЭРОөД¶ЁТеЈәБҪЧйБЪұЯ·ЦұрПаөИөДЛДұЯРОҪРЧцуЭРО. ИзЙПНјЈ¬ЦӨГчЛДұЯРО![]() КЗуЭРО.
КЗуЭРО.
ЈЁ3Ј©ИзНјЈ¬Иф![]() Ј¬ЖдЛыМхјюІ»ұдЈ¬Зу
Ј¬ЖдЛыМхјюІ»ұдЈ¬Зу![]() өДіӨ¶И.
өДіӨ¶И.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
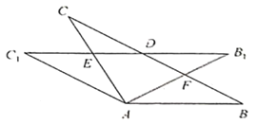
ЎҫМвДҝЎҝИзНјЈ¬ЛДұЯРОКЗХэ·ҪРОЈ¬![]() Ј¬
Ј¬![]() ҙ№Цұ
ҙ№Цұ![]() Ј¬өг
Ј¬өг![]() Ўў
Ўў![]() Ўў
Ўў![]() ФЪТ»МхЦұПЯЙПЈ¬ЗТ
ФЪТ»МхЦұПЯЙПЈ¬ЗТ![]() Ул
Ул![]() ЗЎәГ№ШУЪЛщФЪЦұПЯіЙЦб¶ФіЖЈ®ТСЦӘ
ЗЎәГ№ШУЪЛщФЪЦұПЯіЙЦб¶ФіЖЈ®ТСЦӘ![]() Ј¬Хэ·ҪРОұЯіӨОӘ
Ј¬Хэ·ҪРОұЯіӨОӘ![]() Ј®
Ј®
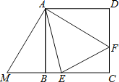
![]() НјЦР
НјЦР![]() ҝЙТФИЖөг________°ҙ________КұХл·ҪПтРэЧӘ________әуДЬ№»Ул
ҝЙТФИЖөг________°ҙ________КұХл·ҪПтРэЧӘ________әуДЬ№»Ул![]() ________ЦШәПЈ»
________ЦШәПЈ»
![]() РҙіцНјЦРЛщУРРОЧҙЎўҙуРЎ¶јПаөИөДИэҪЗРО________Ј»
РҙіцНјЦРЛщУРРОЧҙЎўҙуРЎ¶јПаөИөДИэҪЗРО________Ј»
![]() УГ
УГ![]() Ўў
Ўў![]() өДҙъКэКҪұнКҫ
өДҙъКэКҪұнКҫ![]() Ул
Ул![]() өДГж»эЈ®
өДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ФЪЎчABCЦРЈ¬DКЗBCұЯЙПТ»өгЎП1ЈҪЎП2Ј¬ЎП3ЈҪЎП4Ј¬ЎПBACЈҪ69ЎгЈ¬ЗуЎПDACөД¶ИКэЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРҪбВЫЦРЈ¬ҙнОуөДУР( )
ўЩФЪRtЎчABCЦРЈ¬ТСЦӘБҪұЯіӨ·ЦұрОӘ3әН4Ј¬ФтөЪИэұЯөДіӨОӘ5Ј»
ўЪЎчABCөДИэұЯіӨ·ЦұрОӘABЈ¬BCЈ¬ACЈ¬Иф![]() +
+![]() =
=![]() Ј¬ФтЎПA=90ЎгЈ»
Ј¬ФтЎПA=90ЎгЈ»
ўЫФЪЎчABCЦРЈ¬ИфЎПAЈәЎПBЈәЎПC=1Јә5Јә6Ј¬ФтЎчABCКЗЦұҪЗИэҪЗРОЈ»
ўЬИфИэҪЗРОөДИэұЯіӨЦ®ұИОӘ3Јә4Јә5Ј¬ФтёГИэҪЗРОКЗЦұҪЗИэҪЗРОЈ®
A. 0ёц B. 1ёц C. 2ёц D. 3ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪ![]() ЦРЈ¬өг
ЦРЈ¬өг![]() КЗ
КЗ![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]() ЗТҪ»
ЗТҪ»![]() УЪөг
УЪөг![]() Ј¬ЗуЦӨЈә
Ј¬ЗуЦӨЈә![]() КЗ
КЗ![]() өДЦРО»ПЯЈ®
өДЦРО»ПЯЈ®
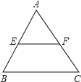
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() Ј¬
Ј¬![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]() КЗ¶ФҪЗПЯЈ¬
КЗ¶ФҪЗПЯЈ¬![]() Ҫ»
Ҫ»![]() СУіӨПЯУЪ
СУіӨПЯУЪ![]() Ј®ИфЛДұЯРО
Ј®ИфЛДұЯРО![]() КЗБвРОЈ¬ФтЛДұЯРО
КЗБвРОЈ¬ФтЛДұЯРО![]() КЗЈЁ Ј©
КЗЈЁ Ј©
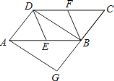
A. ЖҪРРЛДұЯРО B. ҫШРО
C. БвРО D. Хэ·ҪРО
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ![]() КЗ
КЗ![]() өДҪЗЖҪ·ЦПЯЈ¬
өДҪЗЖҪ·ЦПЯЈ¬![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј¬
Ј¬![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј®
Ј®
![]() ЗуЦӨЈәЛДұЯРО
ЗуЦӨЈәЛДұЯРО![]() КЗБвРОЈ»
КЗБвРОЈ»
![]() өұ
өұ![]() ВъЧгКІГҙМхјюКұЈ¬ЛДұЯРО
ВъЧгКІГҙМхјюКұЈ¬ЛДұЯРО![]() КЗХэ·ҪРОЈҝІўЛөГчАнУЙЈ®
КЗХэ·ҪРОЈҝІўЛөГчАнУЙЈ®
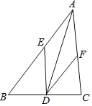
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬AB=ACЈ¬DКЗИэҪЗРОДЪТ»өгЈ¬Б¬ҪУADЈ¬BDЈ¬CDЈ¬ЎПBDC=90ЎгЈ¬ЎПDBC=45ЎгЈ®
(1)ЗуЦӨЈәЎПBAD=ЎПCADЈ»
(2)ЗуЎПADBөД¶ИКэЈ®
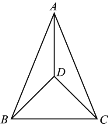
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com