练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，D是BC边上一点∠1＝∠2，∠3＝∠4，∠BAC＝69°，求∠DAC的度数．

    【答案】32°

    【解析】

    设∠1=∠2=x，根据三角形外角的性质可得∠4=∠3=2x，在△ABC中，根据三角形的内角和定理可得方程2x+x+69°=180°，解方程求得x的值，即可求得∠4、∠3的度数，在△ADC中，根据三角形的内角和定理求得∠DAC的度数即可.

    设∠1=∠2=x

    ∴∠4=∠3=∠1+∠2=2x，

    在△ABC中，∠4+∠2+∠BAC=180°，

    ∴2x+x+69°=180°

    解得x=37.

    即∠1=∠2=37°，∠4=∠3=37°×2=74°.

    在△ADC中，∠4+∠3+∠DAC=180°

    ∴∠DAC=180-∠4-∠3=180°-74°-74°=32.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两组同学进行一分钟引体向上测试，评分标准规定，做6个以上含6个为合格，做9个以上含9个为优秀，两组同学的测试成绩如下表：

    成绩个

    　4

    　5

    　6

    　7

    　8

    　9

    　甲组人

    　1

    　2

    　5

    　2

    　1

    　4

    　乙组人

    　1

    　1

    　4

    　5

    　2

    　2

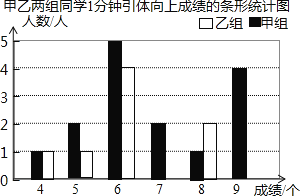
    现将两组同学的测试成绩绘制成如下不完整的统计图表：

    统计量

    平均数个

    中位数

    众数

    方差

    合格率

    优秀率

    甲组

    a

    6

    6

    乙组

    b

    7

    将条形统计图补充完整；

    统计表中的______，______；

    人说甲组的优秀率高于乙组优秀率，所以甲组成绩比乙组成绩好，但也有人说乙组成绩比甲组成绩好，请你给出两条支持乙组成绩好的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，以BC为半径作⊙B，交AB于点D，交AB的延长线于点E，连接CD、CE．
    （1）求证：△ACD∽△AEC；
    （2）当 = 时，求tanE；
    （3）若AD=4，AC=4 ，求△ACE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图①，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，∠ACD是△ABC的外角，∠A=40°，BE平分∠ABC，CE平分∠ACD，且BE、CE交于点E．

    （1）求∠E的度数．

    （2）请猜想∠A与∠E之间的数量关系，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=40°，∠C=80°，AD是BC边上的高，AE平分∠BAC．

    （1）求∠BAE的度数；（2）求∠DAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三角形ABC中，D是边BC上的一点，已知AC=5，AD=6，BD=10，CD=5，那么三角形ABC的面积是（　　）

    A. 30 B. 36 C. 72 D. 125

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的中线，tanB= ，cosC= ，AC= ．求：
    （1）BC的长；
    （2）sin∠ADC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（11分）阳泉同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：32 39 45 55 60 54 60 28 56 41 51 36 44 46 40 53 37 47 45 46

    （1）前10株西红柿秧上小西红柿个数的平均数是 ，中位数是 ，众数是 ；

    （2）若对这20个数按组距8进行分组，请补全频数分布表及频数分布直方图：

    个数分组

    28≤x＜36

    36≤x＜44

    44≤x＜52

    52≤x＜60

    60≤x＜68

    频数

    2




    2

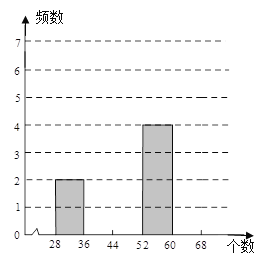
    （3）通过频数分布直方图试分析此大棚中西红柿的长势。

    查看答案和解析>>

    同步练习册答案