
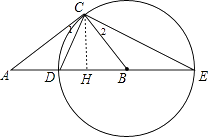
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
【答案】
(1)证明:∵DE为直径,
∴∠DCE=90°,即∠2+∠DCB=90°,
∵∠ACB=90°,即∠1+∠DCB=90°,
∴∠1=∠2,
而∠CAD=∠EAC,
∴△ACD∽△AEC
(2)解:由 ![]() =
= ![]() ,设AC=4k,则BC=3k,
,设AC=4k,则BC=3k,
∴BD=BE=3k,
∴AB= ![]() =5k,
=5k,
∴AE=AB+BE=5k+3k=8k,
在Rt△CDE中,tanE= ![]() ,
,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴tanE= ![]()
(3)作CH⊥AE于H,如图,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得AE=12,CE=
,解得AE=12,CE= ![]() CD,
CD,
∴DE=AE﹣AC=8,
在Rt△CDE中,∵tanE= ![]() =
= ![]() =
= ![]() ,
,
∴∠E=30°,
∴CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,
,
在Rt△CHE中,CH= ![]() CE=2
CE=2 ![]() ,
,
∴△ACE的面积= ![]() ×12×2
×12×2 ![]() =12
=12 ![]() .
.
【解析】(1)利用圆周角定理得到∠DCE=90°,而∠ACB=90°,则∠1=∠2,加上公共角,则可判断△ACD∽△AEC;(2)利用由 ![]() =
= ![]() 设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到
设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到 ![]() =
= ![]() =
= ![]() ,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE=
,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE= ![]() CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD=
CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,接着计算出CH,然后根据三角形面积公式求解.
,接着计算出CH,然后根据三角形面积公式求解.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.

(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
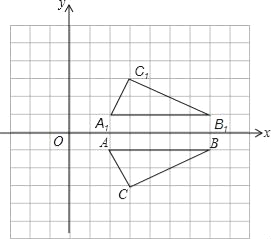
【题目】如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.

(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com