
【题目】如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.
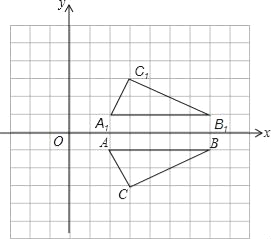
【答案】(1)△ABC是直角三角形;(2)图像向右平移2个单位,C2坐标为(5,2);(3)y=![]() x-
x-![]() ;P(9,0).
;P(9,0).
【解析】
(1)计算出A![]() ,B
,B![]() ,A
,A![]() ,比较数量关系即可;
,比较数量关系即可;
(2)把△![]() 的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
的各顶点的横坐标都加2.纵坐标不变,则图形向右移动两个单位;
(3)连接C![]() ,与x轴的交点即为P,设BC对应一次函数为y=kx+b,联立方程组即可求出点P坐标.
,与x轴的交点即为P,设BC对应一次函数为y=kx+b,联立方程组即可求出点P坐标.
本题解析:
解:(1)∵AC2=22+12=5,BC2=42+22=20,AB2=52
∴AC2+BC2=AB2
∴△ABC是直角三角形
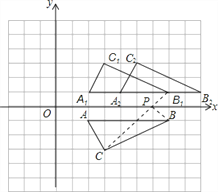
(2)图像向右平移2个单位,C2坐标为(5,2)
(3)存在.连接CB1,与x轴的交点即为P.
理由:设BC对应一次函数为y=kx+b
∵C(3,-3) B(7,-1)
∴![]()
∴
∴y=![]() x-
x-![]()
令y=0得x=9
∴P(9,0)


科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
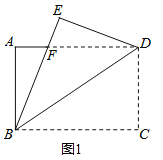
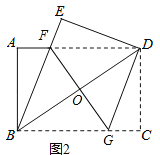
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:BF=DF;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.
①求证:四边形BFDG是菱形;
②若AB=3,AD=4,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)求∠E的度数.
(2)请猜想∠A与∠E之间的数量关系,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com