
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
���𰸡�
��1���⣺������֪�����۹��ȫ���������0��x��100��
��50x��1100��0��
���x��22��
�֡�x��5�ı�����
��ÿ���������������ӦΪ25Ԫ
��2���⣺��ÿ��ľ�����ΪyԪ��
��0��x��100ʱ��y1=50x��1100��
��y1��x�����������
�൱x=100ʱ��y1�����ֵΪ50��100��1100=3900��
��x��100ʱ��
y2=��50�� ![]() ��x��1100
��x��1100
=�� ![]() x2+70x��1100
x2+70x��1100
=�� ![]() ��x��175��2+5025��
��x��175��2+5025��
��x=175ʱ��y2�����ֵΪ5025��
5025��3900��
�ʵ�ÿ�����������Ϊ175Ԫʱ��ÿ��ľ����������5025Ԫ
����������1���۹ȫ�����ÿ��ľ�����=�������г��������멁�����ѣ����ݲ��ȹ�ϵ��������Ϊ�����г�����ʽ��⼴�ɣ���2���ɺ�������ʽ�Ƿֶκ�������ÿһ��������������ֵ���Ƚϵó����������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס�����������ͬ·��ǰ����ѧУ12ǧ�ĵط��μ�ֲ����������ס�������ǰ��Ŀ�ĵ�����ʻ��·��S��ǧ�ף���ʱ��t�����ӣ��仯�ĺ���ͼ����������⣺
��1������ס�����������ʻ��·��S����S����t֮��Ĺ�ϵʽ��
��2������ʻ10���Ӻס�������������ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף��ң�����������ֱ���ɽ�ţ�ɽ����ɽ������������������飬ÿ�������ﲥ�ֶ�ʮ�����ӣ�ũҵר�ҽ�ÿ��������ɻ�����Ӹ���ͳ��������ͳ��ͼ����ͼ��ʾ���������ĸ��ƶϣ� �ټ��������ܻ���Ӱ����С��
����������ƽ���ɻ�����ߣ�
�۱����������ʺϲ�����ɽ����
�����ÿ������ֻ����һ���ط����֣���ôɽ�ţ�ɽ����ɽ���ֱ��ּף��ң�������������ʹ�óɻ�����ߣ�
���к������ǣ� ��
A.�٢�
B.�٢�
C.�ڢ�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����ʾ����1+��2���B+��C��ʲô��ϵ��Ϊʲô��
��2����ͼ�����ѡ�ABCֽƬ��DE���۵�����A�����ı���BCED�ڲ�ʱ�����A�����+����֮����һ��������ϵʼ�ձ��ֲ��䣬��д��������ɲ�˵�����ɣ�
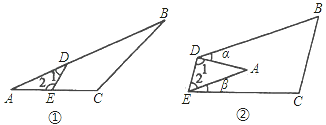
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A=30�㣬BC=2 ![]() ����ֱ�DZ�ACΪֱ������O��AB�ڵ�D����ͼ����Ӱ���ֵ�����ǣ� ��
����ֱ�DZ�ACΪֱ������O��AB�ڵ�D����ͼ����Ӱ���ֵ�����ǣ� �� 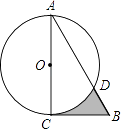
A.![]() ��
�� ![]()
B.![]() ��
�� ![]()
C.![]() ��
�� ![]()
D.![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����ʽ�ķ��ӻ��ĸ������ʽ�ֽ⣬�������ʽ����Լ�֣���ô���dz���
����ʽΪ����г��ʽ��.
��1�����з�ʽ:��![]() ����
����![]() ����
����![]() ����
����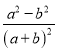 . ����������г��ʽ���� (��д��ż���)��
. ����������г��ʽ���� (��д��ż���)��
��2����![]() ����������
Ϊ����������![]() Ϊ����г��ʽ������д��
Ϊ����г��ʽ������д��![]() ��ֵ;
��ֵ;
��3���ڻ���![]() ʱ��
ʱ��
С����Сǿ�ֱ������������������:
���� ![]()
![]()

Сǿ�� ![]()
![]()
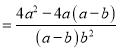
��Ȼ��Сǿ���������еĺ�г��ʽ, ���������ý����С���Ľ����
ԭ���ǣ� ��
�������Сǿ�ķ�����ɻ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʵ��m����m2��m��2=0����m=ʱ������y=xm+��m+1��x+m+1��ͼ����x�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�ž���ֽƬABCD���ŶԽ���BD�����۵�������C�䵽��E����BE��AD�ڵ�F��
��1����֤��BF=DF��
��2����ͼ2������D��DG��BE����BC�ڵ�G������FG��BD�ڵ�O��
����֤���ı���BFDG�����Σ�
����AB=3��AD=4����FG�ij���
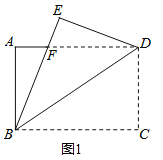
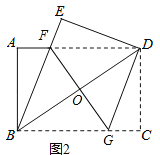
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com