
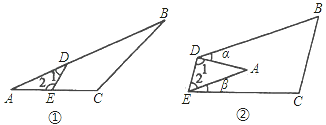
【题目】(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
【答案】(1)∠1+∠2=∠B+∠C;(2)规律:α+β=2∠A.理由见解析
【解析】
(1)根据三角形的内角和是180°,解答即可;
(2)根据题(1)的结论和四边形的内角和是360°解答即可.
(1)∠1+∠2=∠B+∠C,理由如下:
∵如图1,在△AED和△ACB中,
∠1+∠2+∠A=∠A+∠B+∠C=180°(三角形内角和等于180°),
∴∠1+∠2=∠B+∠C(等量代换);
(2)规律:α+β=2∠A,理由如下:
∵在△ADE中,∠1+∠2=180°﹣∠A(三角形内角和等于180°),
在四边形BCED中,∠BDE+∠DEC+∠B+∠C=360°(四边形内角和等于360°),
又∵根据题(1)得∠1+∠2=∠B+∠C(已证),
∴2(∠1+∠2)+α+β=360°(等量代换),
∴2(180°﹣∠A)+α+β=360°(等量代换),
∴α+β=2∠A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
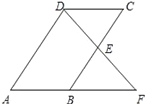
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB. 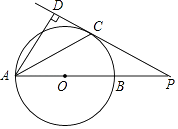
(1)求证:AD⊥PC;
(2)连接BC,如果∠ABC=60°,BC=2,求线段PC的长. 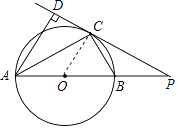
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=2x2+4x+m﹣1,与x轴的公共点为A,B. 
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点; ①当m=1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n<8时,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.

(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com