
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知:10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD. 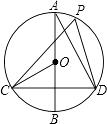
(1)P是 ![]() 上一点(不与C、D重合),求证:∠CPD=∠COB;
上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
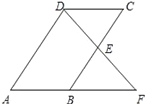
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,深圳今年4 月2 日至4 月8 日每天的最高气温变化如图所示.则关于这七天的最高气温的数据,下列判断中错误的是( ) 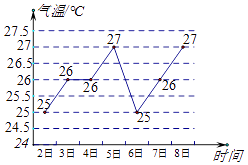
A.平均数是26
B.众数是26
C.中位数是27
D.方差是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):
根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,到
运动,到![]() 点停止.若点
点停止.若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() .如图
.如图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象;图
(秒)的函数关系图象;图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象:
![]() 求
求![]() 、
、![]() 、
、![]() 的值;
的值;
![]() 设点
设点![]() 出发
出发![]() (秒)后离开点
(秒)后离开点![]() 的路程为
的路程为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
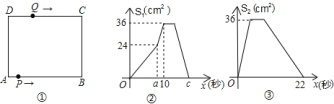
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com