
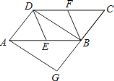
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)

(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用墙为一边,用长为![]() 的材料作另三边,围成一个面积为
的材料作另三边,围成一个面积为![]() 的长方形小花园,这个长方形的长和宽各是( )
的长方形小花园,这个长方形的长和宽各是( )
A. 5m,4m B. 8m,2.5m
C. 10m,2m D. 5m,4m或8m,2.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
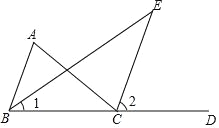
【题目】如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E,以下是小明的证明过程,请在括号里填写理由.
证明:∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知)
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(_________)
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知)
∴∠ACD=2∠2,∠ABC=2∠1(_______)
∴∠A=2∠2﹣2∠1(_________)
=2(∠2﹣∠1)(_________)
=2∠E(等量代换)
(2)如果∠A=∠ABC,求证:CE∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为6的等边三角形,
是边长为6的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
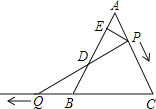
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() ,
,![]() 两种商品,购买
两种商品,购买![]() 个
个![]() 商品比购买
商品比购买![]() 个
个![]() 商品多花
商品多花![]() 元,并且花费
元,并且花费![]() 元购买
元购买![]() 商品和花费
商品和花费![]() 元购买
元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元?
商品各需要多少元?
(2)若商店准备购买![]() ,
,![]() 两种商品共
两种商品共![]() 个,并且购买
个,并且购买![]() ,
,![]() 两种商品的总费用不超过
两种商品的总费用不超过![]() 元,那么商店至多购买
元,那么商店至多购买![]() 商品多少件?
商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
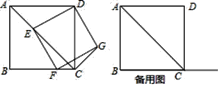
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:矩形
,求证:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
![]() 当线段
当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,直接写出
时,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
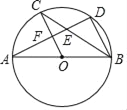
【题目】如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相较于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
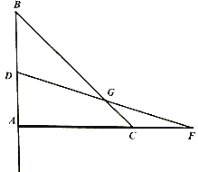
【题目】如图,在等腰![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发,以相同的速度沿射线
出发,以相同的速度沿射线![]() 方向运动,连
方向运动,连![]() ,交直线
,交直线![]() 于点
于点![]()
![]() 当点
当点![]() 运动到
运动到![]() 中点时,求
中点时,求![]() 的长.
的长.
![]() 求证:
求证:![]() .
.
![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,请探究
,请探究![]() 之间的数量关系,并直接写出结论.
之间的数量关系,并直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com